グリーン関数 (グリーンかんすう)
Green function
X,Yを線形関数空間,TをXからYへの線形微分作用素とする。Tが逆作用素T⁻1をもち,それがYの上の積分作用素であるとき,その積分作用素の核をTのグリーン関数という。
例えば,閉区間[a,b]上で2階連続微分可能な関数y(x)で,条件,
(1)αy(a)+α′y′(a)=0,(2)βy(b)+β′y′(b)=0(α,α′,β,β′は定数)
を満たすものの全体をX,[a,b]上で連続な関数の全体をYとすれば,X,Yはともに線形関数空間である。XからYへの2階線形微分作用素,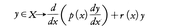 をLで表す。Ly=λy(λは定数)となるような恒等的に0でないy∈Xが存在するとき,λをLの固有値という。lをLの固有値でない定数とすれば,L-lはグリーン関数をもち,それは次の式で与えられる。
をLで表す。Ly=λy(λは定数)となるような恒等的に0でないy∈Xが存在するとき,λをLの固有値という。lをLの固有値でない定数とすれば,L-lはグリーン関数をもち,それは次の式で与えられる。
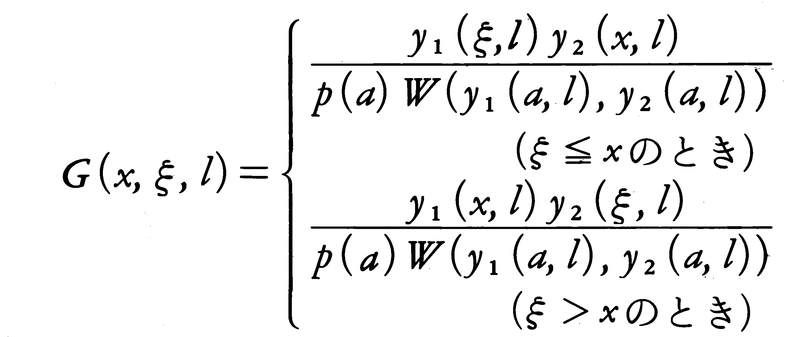
ただし,y1(x,l)は条件(1)を満たす(L-l)y=0の解,y2(x,l)は条件(2)を満たす(L-l)y=0の解で,
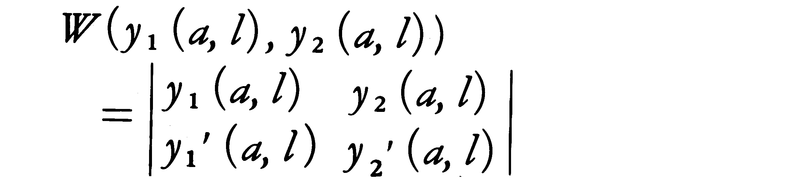
そして(L-l)y=f(f∈Y)の解y(x)∈Xは,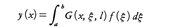 で与えられる。
で与えられる。
執筆者:斎藤 利弥
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
グリーン関数
グリーンかんすう
Green function
微分方程式3次元において,Δ をラプラスの演算子 (ラプラシアン ) とするとき ΔG(x)=-δ(x-ξ) の解は G(x,ξ)=1/4π|x-ξ|-1 で与えられる。この G(x,ξ) をこの微分方程式のグリーン関数という。これを用いると,微分方程式 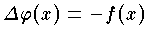 の解は
の解は 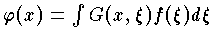 という式で表わせる。一般に楕円型または放物型の偏微分方程式の境界値問題を解くときに,これと類似なグリーン関数を用いる方法が有用である。場の理論では因果関係を明確にするためにグリーン関数が用いられる。統計力学では相関関数または分布関数の拡張とみられる温度グリーン関数が広く用いられる。
という式で表わせる。一般に楕円型または放物型の偏微分方程式の境界値問題を解くときに,これと類似なグリーン関数を用いる方法が有用である。場の理論では因果関係を明確にするためにグリーン関数が用いられる。統計力学では相関関数または分布関数の拡張とみられる温度グリーン関数が広く用いられる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
グリーンかんすう
グリーン関数
Green’s function
ディラックのデルタ関数を非斉次項にもつ線形微分方程式の初期および境界条件を満たす解。ある微分方程式のグリーン関数が既知であれば,任意の非斉次項に対するその微分方程式の解をグリーン関数の重ね合わせで記述できる。地震学においては,震源における断層すべりに伴う等価体積力や,津波をもたらす初期海面水位などに対する解などをグリーン関数として扱う。ただし実用上は,厳密なデルタ関数に対する応答ではなく,有限の時間・空間幅をもつ基底関数を非斉次項にもつ微分方程式の解をグリーン関数と呼ぶことも多い。
執筆者:前田 拓人
出典 平凡社「最新 地学事典」最新 地学事典について 情報
Sponserd by 
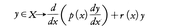 をLで表す。Ly=λy(λは定数)となるような恒等的に0でないy∈Xが存在するとき,λをLの固有値という。lをLの固有値でない定数とすれば,L-lはグリーン関数をもち,それは次の式で与えられる。
をLで表す。Ly=λy(λは定数)となるような恒等的に0でないy∈Xが存在するとき,λをLの固有値という。lをLの固有値でない定数とすれば,L-lはグリーン関数をもち,それは次の式で与えられる。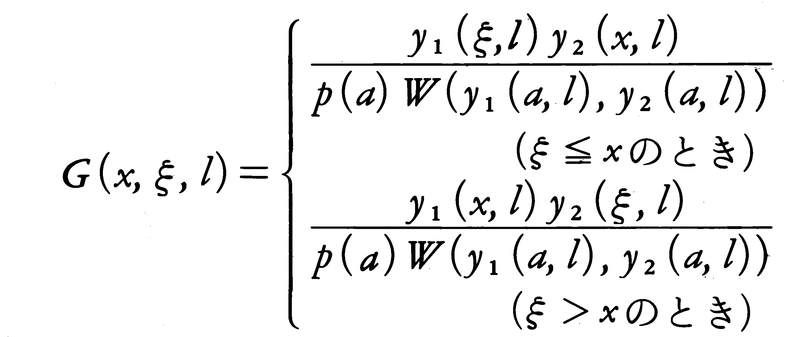
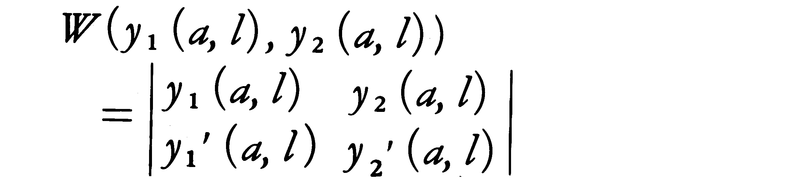
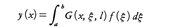 で与えられる。
で与えられる。

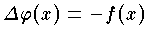 の解は
の解は 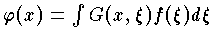 という式で表わせる。一般に楕円型または放物型の
という式で表わせる。一般に楕円型または放物型の