演算子（読み）エンザンシ（英語表記）operator

デジタル大辞泉

えんざん‐し【演算子】

１ ある集合の元げんに他の集合の元を対応させる一定の演算記号。例えば微分方程式において、関数を導関数に対応させる記号d/dtなど。作用素。
２ 《operator》⇒オペレーター6

出典　小学館

精選版 日本国語大辞典

えんざん‐し【演算子】

〘名〙 関数に関数を対応させる写像。微分法、積分法など。作用素。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

演算子
えんざんし
operator

作用素ともいい、一般には写像とほぼ同義の内容をもつ。とくに線形空間や関数空間で用いられることが多く、たとえば関数f(x)を他の関数g(x)に変換するとき、それを
　　g(x)＝Tf(x)
のように書いて、Tを演算子という。演算子はしばしば一定の計算規則で指定されている。たとえば、演算子法でよく用いられる微分演算子Dは関数f(x)を微分してf′(x)をつくることを意味し
　　Df(x)＝f′(x),
　　　D²f(x)＝D［Df(x)］＝f″(x),……
である。

　空間の点（x,y,z）で定義された関数f(x,y,z)では偏微分が問題になるが、ベクトル解析の記法として、次のような演算子がよく用いられる。

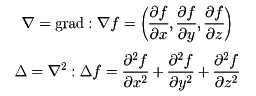
∇はナブラと読み、∇fは関数fの勾配(こうばい)ベクトル、Δはラプラシアン（ラプラス演算子）という。また、点（x,y,z）にベクトルの値
　　V(x,y,z)＝(f(x,y,z),g(x,y,z),h(x,y,z))
を対応させる関数に対し、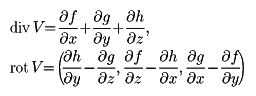

によって、演算子div（発散）とrot（回転）を定義すると、
　　divV＝(∇,V),
　　rotV＝∇×V
などの関係があり、演算子∇をベクトルと同様に取り扱うことができる。

［洲之内治男］

物理学における演算子

数学のさまざまな概念や手法は可能な限り物理学のなかで用いられてきた。演算子もその一つであるが、とくに電気工学者であったヘビサイドが電気回路の解析をきっかけに演算子法を開拓したという事情もあり、今日物理学のなかで演算子は非常に多彩に用いられている。物理学のほとんどの部分が線形物理学であるから、物理学に表れる演算子は多く線形演算子であり、線形空間あるいは関数空間の一次写像として扱われる。

　演算子がとくに重要な役割をもつのは量子力学の分野である。量子力学では、測定により得られる結果は確率的なので、「ある量」とその「測定値」とは区別されなければならない。このため状態を表す関数（状態関数）と、それに作用する「ある量」を表す演算子を考える。演算子を作用させた結果が定まった数値を与える場合はとくに重要で、このような場合、演算子は「物理量」を表している。すなわち、一つの測定の結果がかならず一義的に定まっている。これが量子力学における測定の基礎を与える。このときの状態はその物理量の固有状態といわれ、演算子の固有関数である。そして一般の状態はこれら固有状態の重ね合わせで表される。このように、量子力学ではすべての物理量は演算子で表され、その演算子は重ね合わせの原理により線形であり、また観測値はすべて実数であるという要請から自己共役(きょうやく)性（エルミート性）をもつ。

　演算子は一般に作用させる順序を交換できないから、それで表される二つの物理量は、順序を入れ替えて状態に作用させたとき、等しい結果を与えない。すなわち同じ測定値は得られない。このことが不確定性原理の内容であり、とくに二つの演算子が交換可能な特別の場合にだけ、その二つの物理量は同時に観測可能となる。

［藤村　淳］

[参照項目] | 演算子法 | 写像 | ベクトル解析

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

演算子
えんざんし
operator

一つの関数f（x）に対してほかの関数 g（x）を一定の規則に従って対応させる演算 f→g を表す演算記号。オペレーターの訳語であり，伝統的に物理学においては演算子と呼ばれ，数学においては作用素と呼ばれる。g（x）＝（d/dx）f（x）のように微分の操作を含む演算子を微分演算子という。また，演算子 O が O（f＋g）＝Of＋Og ，O（cf）＝cOf（c は任意の数）という関係を満たすときの O を，線形演算子（線形作用素）または一次演算子という。二つの演算子 O₁，O₂があり，g＝O₁f，h＝O₂g であるとき，h＝Of で定義される演算子 O を O₁と O₂の積と呼び，O＝O₂O₁と書く。このように定義された積は，一般に交換可能ではなく，O₂O₁≠O₁O₂である。量子力学では，位置や運動量のような物理量は演算子で表現されるため，演算子が一般に交換可能でないことは重要な意味をもつ。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

演算子【えんざんし】

作用素とも。数学，物理学，工学で使う演算（変換）を表す記号。数や式の乗法，微分，積分，ベクトル解析のラプラス演算子▽²，勾配(こうばい)grad，発散div，回転rotなど種々ある。演算子を用いて微積分の問題などを代数形式で解く方法を演算子法といい，特にヘビサイドが電気回路の計算に応用した。また量子力学では物理量はシュレーディンガーの波動関数に作用する演算子の形をとる。
→関連項目写像

出典　株式会社平凡社

ASCII.jpデジタル用語辞典

演算子

プログラミング言語上で、計算の内容を表す記号のこと。オペレーターとも呼ばれる。演算子の種類は、算術演算子（「+」、「-」など）、関係演算子（「＝」、「」など）、論理演算子（「AND」、「OR」、「&&」、「||」）などがある。演算の対象となる値や変数のことは、オペランドという。

出典　ASCII.jpデジタル用語辞典

世界大百科事典（旧版）内の演算子の言及

【演算子法】より

…関数に対する微分や積分の演算を記号的，あるいは代数的に行い，微分方程式を形式的に解く手法を演算子法という。19世紀の終りころに，イギリスの工学者O.ヘビサイドが電気工学におけるいろいろな現象を記述する常微分方程式や，電信方程式と呼ばれる偏微分方程式を解くのにこの手法で成功をおさめて以来，演算子法はまとまった一つの理論となった。…

【関数解析学】より

…また連続関数の列の一様収束の極限は連続関数であるから，Cにおける収束とは関数列の一様収束のことであると約束することにより，ふつうのユークリッド空間における点列の収束と同様な取扱いができる。さらに，関数を微分する操作や積分する操作を関数から関数への対応と考え，このような対応を作用素，または演算子という。このようにベクトル算法と収束概念の定義された空間の構造や，その空間における作用素の性質を一般的に調べることにより，従来は別個のものと考えられてそれぞれの方法で取り扱われていたいくつかの理論が，統一された簡単な方法で，より一般的に扱われるようになり，また他方において，多くの新しい事実を導くことができるようになった。…

【量子力学】より

…は，たとえば水素原子の電子の場合でいえば，電子の質量をm，電荷を－e，真空の誘電率をε₀として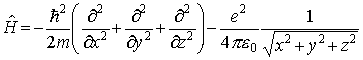，の形であり，電子の位置座標に相当するr＝(x,y,z)の関数ψ_t＝ψ_t(x,y,z)に作用してこれを別の関数に変える働きをもつ。この種の働きをもつものを一般に演算子とよぶ。そのもっとも単純なものは関数をxで微分する微分演算子∂/∂xである。…

※「演算子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」