境界値問題（読み）きょうかいちもんだい

日本大百科全書(ニッポニカ)

境界値問題
きょうかいちもんだい

微分方程式に関し、ある領域で微分方程式を満たし、この領域の境界で与えられた条件を満たす解を求める問題を境界値問題という。このとき境界上で与えられた条件を境界条件という。二階常微分方程式
　　(p(x)y′)′＋(q(x)＋λ)y＝0
を区間［a,b］上で考え、境界条件
　　αy(a)＋βY′(a)＝0
　　γy(b)＋δy′(b)＝0
を課した境界値問題をスチュルム‐リウビルの問題という。ただしp(x)は正値で、α²＋β²とγ²＋δ²は0でないとする。またλはパラメーターである。これは、たとえば弦の定常振動を記述する関数を求める問題として現れる。そのためパラメーターλに対し、境界値問題の0でない解を求める問題が重要である。これを固有値問題という。λに対し0でない解があるときλを固有値、その0でない解を固有関数という。いまの場合、固有値は可算無限個あり、それらをλ_nとするとλ₀＜λ₁＜……＜λ_n＜……と並べることができて、λ_n→∞(n→∞)となる。各λ_nに対する固有関数は定数倍することを除いて一意的に定まる。その一つをψ_n(x)とすると、関数列｛ψ_n(x)｝は区間［a, b］において完備直交列をなす。0が固有値でないとすると適当な関数G(x,ξ)が存在して、与えられたf(x)に対し
　　(p(x)y′)′＋q(x)y＋f(x)＝0
の解で、前記の境界条件を満たすものは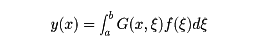

で与えられる。このG(x,ξ)をグリーン関数という。このときスチュルム‐リウビルの問題は、積分方程式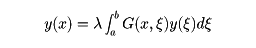

の解を求める問題と同等になり、積分方程式の理論が適用される。

　偏微分方程式についても境界値問題が考えられる。固有値問題としては、たとえばDを三次元空間の有界領域でその境界Sが十分滑らかであるとき、Dで方程式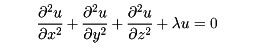

を満たし、S上で0となる解uを求める問題がある。固有値、固有関数の概念が常微分方程式の場合と同様に定義され、この場合も固有値は可算無限個で、それらは
　　λ₁＜λ₂＜……＜λ_n＜……,
　　λ_n→∞ (n→∞)
となる。各λ_nに対し一次独立な固有関数は有限個しかない。これらをψ_n, ₁(x),……,ψ_n, _m(n)(x)とすると、関数列
　　｛_n,j(x) ; j＝1, 2,……, m(n), n＝1, 2,……｝
はD上の完備直交関数列になる。

［小林良和］

[参照項目] | 固有値

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

境界値問題
きょうかいちもんだい
boundary value problem

微分方程式で，特に変分問題と関連した場合など，初期条件から考える初期値問題と異なって，たとえば d²x/dt²＝λx，x(0)＝0，x(π)＝0 のように区間 [0，π] の境界での値で考えねばならない問題がある。偏微分方程式になると，たとえば x²＋y²≦1 という円板で ∂²u/∂x²＋∂²u/∂y²＝0，u( cos θ，sin θ)＝f(θ) というように，境界値 f(θ) から u を求めようといった問題が典型的に生じる。こうした問題を境界値問題という。境界値問題は，微分作用素の固有値問題と関係が深い。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の境界値問題の言及

【境界条件】より

…微分方程式は一般に無数の解をもつが，その定義されている領域の境界上で解，あるいはそれの導関数の値に対して何等かの条件を課すことによって，一つの解を指定することができる。この条件を境界条件，境界条件を満たす解を求めることを境界値問題boundary value problemという。これは振動論，ポテンシャル論など，多くの物理的な問題に関連してしばしば現れる問題である。…

※「境界値問題」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」