分布関数（読み）ブンプカンスウ

デジタル大辞泉

ぶんぷ‐かんすう〔‐クワンスウ〕【分布関数】

統計学や確率論において、ある変数に対する度数や数量を表す関数。正規分布や二項分布などのグラフを曲線で表したとき、その曲線を定義づける関数をさす。また、このグラフの曲線を分布曲線という。

出典　小学館

日本大百科全書(ニッポニカ)

分布関数
ぶんぷかんすう

種々の年齢xに対する人口数yを表したものを人口分布というように、ある変数xに対してその分布数yとの関係を分布関数という。分布関数には不連続分布と連続分布がある。賽(さい)を何度も振って、1から6の目が何回出るのかを数えるとき、その分布は整数1,2,……,6に対する回数で、不連続分布である。一方、気体分子の速さの分布のように、速さは実数で連続であるから連続分布となる。分布は速さがvからv＋dvの微小区間の分子数で表す。

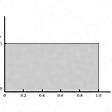
　賽を振った数（試行数）をNとし、賽の目iが出現した回数をN_iとすれば、出現確率P_iはN_iをNで割ったP_i＝N_i/Nで定義され、とくに細工をしない限り試行数Nが十分大きいとき、すべて同じ確率P_i＝1/6となると信じられている。これを確率分布といい、図Aに示す。0から9までの数字をランダムに並べた乱数表では、各数字の出現確率は1/10である。

　数値シミュレーションでよく用いられる[0,1]間の実数乱数は連続分布の例である。得られたすべての実数から、xからx＋dxの間に現れる実数の出現数をy(x)とすれば、試行数Nで割った分布P(x)＝y(x)/Nを確率分布関数という。実数乱数の分布数がxの値によらず、同じであるとき、この分布を一様分布といい、この乱数は[0,1]間の一様実数乱数という。これを図Bに示す。

　確率分布においては、不連続分布の場合、すべての出現確率の和Σ_iP_i＝1、また連続分布の場合、確率分布関数の積分値ʃP(x)dx＝1が満たされている。

［小野昱郎］

正規分布

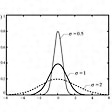
もっともよく知られている分布の一つに、次の正規分布がある。ガウス分布ともよばれている。的をねらって撃った弾丸の着弾位置が的の周りに分布する。ある量を精密に何度も測定すると、その測定値の分布は特定の値の周り左右対称にピークができることが知られている。正規分布はx₀を特定の値として、xの値がxからx＋dxの間に出現する確率をP(x)とすれば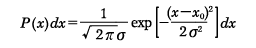

で与えられる。x＝x₀で、この分布関数は最大値をとる。またx₀はこの分布の平均値でもある。σ(シグマ)は分散または標準偏差といわれ、(x－x₀)²の平均値の平方根である。σは分布関数の幅を表し、x＝x₀±σでの分布関数の値は最大値の約0.60である。±σの範囲内に全確率の68％が含まれ、また±2σの範囲には全確率の95％が含まれる。図Cに正規分布関数が示されている。図からもわかるように、σが小さいほど分布関数の山は鋭く高くなり、分布は平均値x₀付近の値をとる確率が高くなる。

　気体分子の速度も正規分布で表されることが知られている。気体の分子の重心速度のx成分をv_xとすれば、その速度がv_xからv_x＋dv_xの範囲にある確率分布は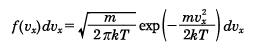

のように与えられる。ここで、mは気体分子の質量、kはボルツマン定数、Tは気体の絶対温度である。分子速度のx成分の平均値は0であるが、標準偏差σが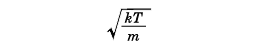

であるので、温度の上昇につれて、速度分布の幅は広がる。三次元速度成分(v_x,v_y,v_z)がv_x～v_x＋dv_x、v_y～v_y＋dv_y、かつv_z～v_z＋dv_zの間にある確率分布は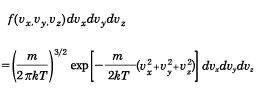

となる。これをマクスウェルの速度分布則という。試験の点数の分布も、かならずしも正規分布ではないが、正規分布を援用して議論されることも多い。

［小野昱郎］

二項分布

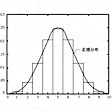
統計でよく現れる分布の一つに二項分布がある。コインを無作為に投じたとき、表裏の現れる確率はそれぞれ1/2であるが、コインをN回投げたとき、表がm回出る確率をP(m;N)とすると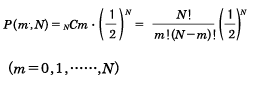

と表される。ここで、！は階乗、N!＝N(N－1)(N－2)……2・1を表す。例としてN＝10のときの分布を図Dに示す。Nが十分大きいとき、この分布の最大値付近は正規分布と同じになることが知られている。

［小野昱郎］

指数分布

放射性元素が放射線を出して崩壊していくとき、もとの元素の原子数は時間がたつとともに減少していく。その数は指数分布で記述される。時刻0のときの放射性原子数をn₀とすれば、時刻tでの原子数n(t)は
　　n(t)＝n₀exp(－t/τ)
のように表される。τを平均寿命という。これを図Eに示す。時刻t＝τではもとの原子核数の約37％になる。原子核の数がもとの半分になる時間を半減期といい、0.693τで与えられる。

　ほかに物理現象では、気体分子の衝突時間間隔などはポアソン分布で表され、共鳴型吸収曲線はローレンツ分布となる。

［小野昱郎］

　数学的には、確率変数Xに対して、実数xの関数
　　F(x)＝P(X≦x)
をXの分布関数という。すなわちF(x)はXの値がx以下である確率を表す。F(x)は次の性質をもつ。

　また、確率とは無関係に、（－∞,∞）で定義された実数値関数F(x)で、前記の(1)、(2)、(3)の性質をもつものを分布関数ということもある。分布関数F(x)の不連続点はたかだか可算個である。ここでは一次元分布関数について述べたが、n次元確率変数（X₁,X₂,……,X_n）の分布関数というのは、n変数の関数
　　F(x₁,x₂,……,x_n)
　　　＝P(X₁≦x₁,X₂≦x₂,……,X_n≦x_n)
のことである。

［古屋　茂］

賽の目の出現確率分布〔図A〕

[0：1]の間の一様実数乱数の出現確率…

正規確率分布〔図C〕

二項確率分布〔図D〕

指数分布〔図E〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

分布関数
ぶんぷかんすう
distribution function

確率変数 X について，Pr(X≦x)＝F(x) とおけば，F(x) は x の関数であるが，これを確率変数 X の分布関数，または累積分布関数という。分布関数 F(x) は次の性質をもっている。
(1) x₁＜x₂ ならば，F(x₁)≦F(x₂)
(2) n→∞ のとき F(x)→1 ，n→－∞ のとき F(x)→0
(3) F(x) は右方連続である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の分布関数の言及

【確率分布】より

…実数値をとる確率変数Xに対してF(x)＝P(X≦x)とおき，これをXの分布関数という。それは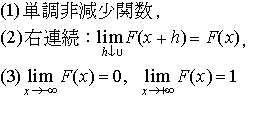，である。…

【ボルツマン方程式】より

…気体分子の分布関数を決定するための基礎的な方程式で，1872年，L.ボルツマンにより導かれた。気体中の1個の分子の運動状態を決めるには，空間座標x,y,zと運動量成分p_x,p_y,p_zとを指定すればよい。…

※「分布関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」