ロルの定理 (ロルのていり)
Rolle's theorem
関数f(x)が閉区間[a,b]で連続,かつ開区間(a,b)で微分可能であって,f(a)=f(b)ならば,f′(c)=0となる点cが開区間(a,b)の中に存在する。これをロルM.Rolle(1652-1719)の定理という。この事実は幾何学的には,関数f(x)が[a,b]における最大値をとる点,または最小値をとる点のうち,両端の点a,bに一致しない点の一つをcとすると,y=f(x)のグラフ上でx=cに対応する点における接線の傾きが0であることを意味する(図1)。上の定理でf(a)=f(b)という仮定を除いた場合は,
f(b)-f(a)=(b-a)f′(c)
となる点cが(a,b)の中に存在する。これを微分法における平均値の定理という(図2)。平均値の定理はロルの定理を使って証明され,また平均値の定理から,関数の増減・極大・極小を調べること,テイラー展開など微分法に関するいろいろの重要な事実が導かれる。
→微分
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
法則の辞典
「ロルの定理」の解説
ロルの定理【Rolle's theorem】
閉区間(a,b)において f(x)が連続で,a<x<b なるすべての x について f′(x)が存在する場合,もし f(a)=f(b)=0であるならば,a<x<b の少なくとも一つの値 x において f′(x)=0である.
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のロルの定理の言及
【微分】より
… この定理でf(a)=f(b)という特別な場合はロルRolleの定理と呼ばれる。平均値の定理の証明はロルの定理に帰着され,ロルの定理は,有限閉区間で連続な関数はその区間で最大値,最小値をとる,という定理を用いて証明される。平均値の定理は幾何学的には,y=f(x)のグラフの上の2点A(a,f(a))とB(b,f(b))とを結ぶ直線に平行な接線が引けるような点Cが,グラフ上でAとBとの間にあることを意味する(図3)。…
【平均値の定理】より
…(1),(2)をそれぞれラグランジュの平均値定理,コーシーの平均値定理というが,単に平均値定理といえば(1)を指す。(2)でg(x)≡xの場合が(1)であり,(1)でさらにf(b)=f(a)の場合はロルの定理と呼ばれる。
[積分法における平均値の定理]
(1)a≦x≦bにおいてf(x)は連続であり,またg(x)は積分可能であって符号が一定ならば,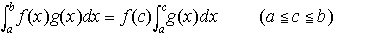 なるcが存在する。…
なるcが存在する。…
※「ロルの定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 



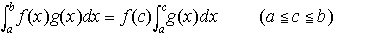 なるcが存在する。…
なるcが存在する。…