改訂新版 世界大百科事典 「グリーン関数」の意味・わかりやすい解説
グリーン関数 (グリーンかんすう)
Green function
X,Yを線形関数空間,TをXからYへの線形微分作用素とする。Tが逆作用素T⁻1をもち,それがYの上の積分作用素であるとき,その積分作用素の核をTのグリーン関数という。
例えば,閉区間[a,b]上で2階連続微分可能な関数y(x)で,条件,
(1)αy(a)+α′y′(a)=0,(2)βy(b)+β′y′(b)=0(α,α′,β,β′は定数)
を満たすものの全体をX,[a,b]上で連続な関数の全体をYとすれば,X,Yはともに線形関数空間である。XからYへの2階線形微分作用素,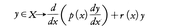 をLで表す。Ly=λy(λは定数)となるような恒等的に0でないy∈Xが存在するとき,λをLの固有値という。lをLの固有値でない定数とすれば,L-lはグリーン関数をもち,それは次の式で与えられる。
をLで表す。Ly=λy(λは定数)となるような恒等的に0でないy∈Xが存在するとき,λをLの固有値という。lをLの固有値でない定数とすれば,L-lはグリーン関数をもち,それは次の式で与えられる。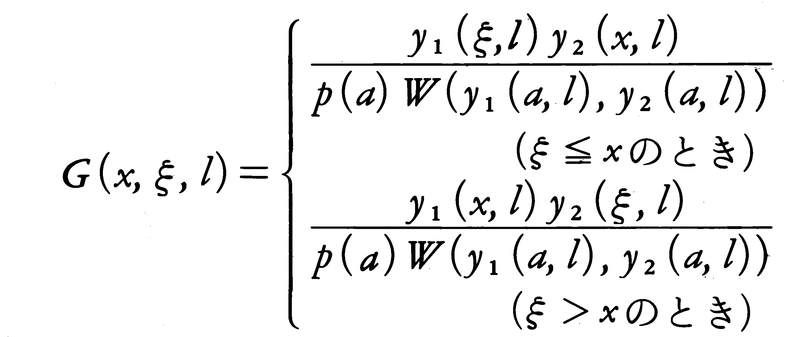
ただし,y1(x,l)は条件(1)を満たす(L-l)y=0の解,y2(x,l)は条件(2)を満たす(L-l)y=0の解で,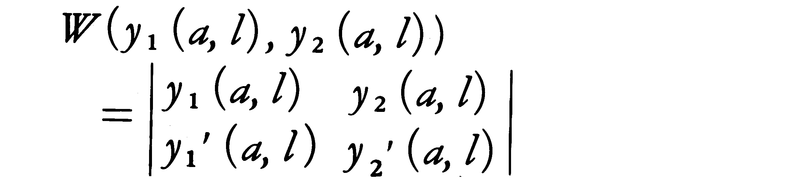
そして(L-l)y=f(f∈Y)の解y(x)∈Xは,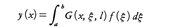 で与えられる。
で与えられる。
執筆者:斎藤 利弥
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


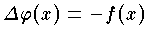 の解は
の解は 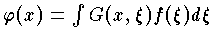 という式で表わせる。一般に楕円型または放物型の
という式で表わせる。一般に楕円型または放物型の