チェビシェフの不等式（読み）チェビシェフのふとうしき（英語表記）Chebyshev's inequality

改訂新版　世界大百科事典

チェビシェフの不等式 (チェビシェフのふとうしき)
Chebyshev's inequality

確率変数Xの分布がどのようなものであれ，有限な平均値mと標準偏差σをもつときは，Xの値が平均値と絶対値においてtσ以下の違いしかないような確率は，1－1/t²よりも大きい。式で表せば，

　P（｜X－m｜＜tσ）＞1－1/t²

となる。これをチェビシェフの不等式という。

　これは簡単な評価式であるが，mとσさえわかれば，σを尺度としてXがどの程度の大きさならその確率はどれほどになるかという大略の見当をつけるのに便利な式である。また，ベルヌーイ型の大数の（弱）法則の証明に用いられるなど確率論でたいせつな役割を果たしている。

　この一般化としては，m_kを平均値のまわりのk次絶対モーメント（m_k＝E｜X－m｜^k）として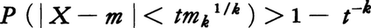，などがある。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

チェビシェフの不等式
チェビシェフのふとうしき
Chebychev's inequality

確率変数を x ，x の平均値を μ ，正の分散を σ² とするとき，任意の正の数 ε に対して ｜x－μ｜≧ε となる確率は σ²/ε² より大きくない。すなわち確率の記号を使って式に表わせば Pr(｜x－μ｜≧ε)≦σ²/ε² である。この式をチェビシェフの不等式という。関数解析的にいえば，平均収束と測度収束の関係を表わしている。

出典　ブリタニカ国際大百科事典 小項目事典