確率論（読み）カクリツロン（英語表記）probability theory

デジタル大辞泉

かくりつ‐ろん【確率論】

偶然事象に関して、その起こる確率の理論と応用を研究する数学の一部門。公算論。

出典　小学館

精選版 日本国語大辞典

かくりつ‐ろん【確率論】

1. 〘 名詞 〙 確率の理論と応用を研究する数学の一分科。ソ連の数学者コルモゴロフによって、理論的基礎が築かれ、近代統計学にも重要な役割を果たしている。
   1. [初出の実例]「確率論的の考察からもいちばん考えやすい事であるが」(出典：比較言語学に於ける統計的研究法の可能性に就て（1928）〈寺田寅彦〉)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

確率論 (かくりつろん)
probability theory

偶然現象の起こる確率を数学的に取り扱い，その応用を考える数学の一分科。17世紀にフランスの数学者B.パスカル，P.フェルマー，オランダのC.ホイヘンスなどがゲームに必要な確率の計算をしたり，平均値の概念を導入したりしたのが，確率を系統的に扱った最初といわれる。18世紀になって，独立な試行を何回も繰り返した（ベルヌーイ試行という）ときの大数の法則を認識したのがスイスの数学者ヤコブ・ベルヌーイ（1654-1705）であった。そこでは，頻度は試行回数を増やすとしだいに真の確率に近づいていくことが示された。次いで訪れたのは，フランスのP.ラプラスやドイツのC.F.ガウスらによって数学的理論の基礎的内容が形成され豊かな応用が見いだされた時代である。ラプラスは1812年に《確率の解析的理論》を著し確率分布や極限定理などを解析的に論じた。ガウスは測量や天文観測の際，測定誤差を処理して真の値を正確に知るために最小二乗法を創始し発展させたが，これらは18世紀後半から19世紀にかけてであった。19世紀までの確率論はいわゆる古典確率論と呼ばれ，それぞれ興味ある固有の理論を作り上げてきたといえる。

　今世紀になって，集合論をはじめとする近代数学を駆使することによって，その基礎が厳密な論理のうえに打ち立てられ，取り扱いうる内容を飛躍的に豊かにした。ソ連のA.N.コルモゴロフは，1933年その著書《確率論の基礎概念》で確率論の出発点となる確率空間の概念を導入し，近代確率論の発生に大きく貢献した。その空間は根元事象ωの集りであるΩ，その部分集合である事象を集めた族B，事象Aの確率P（A），A∈Bからなる。そして確率変数は，Ωの上のB-可測な関数X（ω），すなわちXがある値をとる（ωの集合に）確率が定義されるような関数である。こうした基礎のうえに確率論は極限定理，確率過程論，数理統計学への応用等々数学の一分野として確立された。

　同じ分布に従う独立な確率変数の和を規格化（平均値を0に，分散を1にするよう適当な数を引いたり割ったりすること）すれば，変数の個数が多いときその分布は標準正規分布に近いとする中心極限定理，また関連した極限定理はソ連のヒンチンA.Y.Khintchin（1894-1959）をはじめ多くの学者によって研究された。また時間の推移とともに変化する偶然現象を扱う確率過程の研究は，近代確率論のもっとも重要な課題となっている。1905年にA.アインシュタインが数学的理論を与えたブラウン運動も，その後，ガウス型の典型的な確率過程として認識され，フランスのP.レビをはじめ多くの人々によって研究された。より一般の確率過程論の方向は，ある一時点での情報を知れば過去と未来は独立になるというマルコフ過程，とくに拡散過程の研究で，伊藤清，アメリカのフェラーW.Fellerらによって集大成された。多次元への移行においてはまだ多くの研究課題を残している。定常過程，時系列などの方向はN.ウィーナーの貢献が大きい。特筆すべきことは，これらの研究は数学内の他分野と密接に関連するばかりでなく，確率過程がゆらぎやノイズをもモデルとしうることから，物理学，生物学，工学などと深い交流を保っているということである。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

確率論
かくりつろん
theory of probability

不確定な偶然現象，すなわち起りうる可能性がいくつかあって，そのどれが起るか断言できない場合について，その「確からしさ」を研究する数学的理論。1つの事象の起りうる可能性全体の集合を標本空間 S とし，S の元すなわち各可能性 e_i ( i＝1 ，2，…) 標本点，S の部分集合 A を事象ということにする。 S＝{e_i} ( i＝1 ，2，…) が与えられたとき各 e_i の起る確率とは，各 e_i に負でない実数 p_i を対応させ，Σp_i＝1 であるようにしたときのこの p のことと定義し，p_i＝Pr(e_i) と書く。また事象 A の確率とは，A に属する e_i について起る確率の和のことで，これは Pr(A)＝ΣPr(e_i) で表わす。ただし，これは標本空間 S の標本点 e_i が離散的になっている場合なので，さらに解析学と結合させるためには，これが連続的である場合を考えなければならない。このことから，確率論は，ある標本空間が与えられたとき，その上にどのような確率を定め，そこからどのような結果が得られるかを研究する学問ともいえる。確率論を数学として体系づける最も論理的な行き方は，直観的な要素の助けをかりずに，確率をある公理系を満たす量と考えた A.コルモゴロフの提唱による方法である。標本空間 (抽象的な元の集合) を S ，S の部分集合を事象と呼ぶとき，S のおのおのの事象 A に対して，次の公理を満足するような Pr(A) を対応させ，この Pr(A) を事象 A の確率と定義する。
(1) Pr(S)＝1
(2) 0≦Pr(A)≦1
(3) A_i∩A_j＝φ(i≠j) ならば
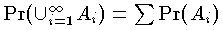
以上が確率の公理的定義である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の確率論の言及

【確率】より

…銅貨を投げて表が出たり裏が出たりするのは同じ程度に期待できるとか，明日は雨がほとんど降ることはなかろうなど，偶然に支配されて起こる事柄について，それが起こる可能性の大小を表す数値が確率である。そしてそのような現象を数学的に取り扱うのが確率論である。実際の具体的な現象では偶然に起こる事実に加えて他のいろいろな要因が関係してきて複雑になるので，理想化したモデルを想定して考えることが多い。…

【統計学】より

…また計量生物学と呼ばれるもののなかには，農業，医学，薬学，生態学などへの応用も含まれ，それぞれ独立した応用分野となりつつある。
【統計学の歴史】
　統計学の前身として，ふつう政治算術political arithmetic，国状論Staatenkunde，確率論の三つがあげられる。いずれも17世紀にそれぞれイギリス，ドイツ，フランスで生まれたものである。…

※「確率論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」