標準偏差（読み）ヒョウジュンヘンサ（その他表記）standard deviation

デジタル大辞泉

ひょうじゅん‐へんさ〔ヘウジユン‐〕【標準偏差】

資料の散らばりの度合いを示す数値。各資料の値と平均値との差、すなわち偏差の2乗を平均し、その正の平方根をいう。変動に富む現象について、変動の度合いを知るために用いる。SD（standard deviation）。

出典　小学館

精選版 日本国語大辞典

ひょうじゅん‐へんさヘウジュン‥【標準偏差】

1. 〘 名詞 〙 統計データや確率変数の値の散らばりの度合を示す数値の一つ。分散の平方根のうち負でないものをいい、ふつうσ(シグマ)で表わす。標準誤差。ＳＤ。〔推計学の話（1949）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

標準偏差
ひょうじゅんへんさ
standard deviation

標準偏差は、一群の観測値または測定値に対して使用される場合と、確率変数に対して使用される場合の二通りがある。

(1)観測値または測定値の標準偏差　n人のクラスであるテストが行われ、各人の点数をx₁、x₂、……、x_nとする。算術平均をx^-で表す。

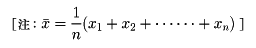
このとき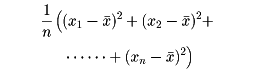

を分散といい、分散の平方根を標準偏差という。標準偏差の値が小さいときは、n個の点数は一つの値の近くに固まった形となる。極端な場合として標準偏差が0であれば、各x_iはすべて同じ値となる。また標準偏差の値が大きいとき、点数は全体として散らばった形となる。すなわち、標準偏差は一群の観測値または測定値の散らばりの度合いを表すものである。

(2)確率変数の標準偏差　Xを離散型確率変数とする。すなわち、Xのとりうる値がx₁、x₂、……であって、Xがx_iという値をとる確率p_iについてp_iの総和は1であるとする。

　このとき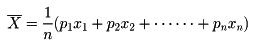

を確率変数Xの平均値という。また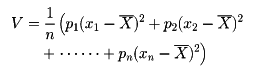

を確率変数Xの分散といい、分散の平方根を確率変数Xの標準偏差という。

　次にXが連続型の確率変数の場合を考えよう。いま連続関数f(x)があって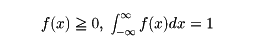

を満たし、Xの値が区間Jに属する確率が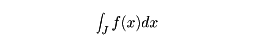

で与えられるとき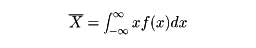

を確率変数Xの平均値という。また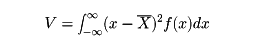

を確率変数Xの分散といい、分散の平方根を確率変数Xの標準偏差という。

　次に一般の確率変数Xについて考える。Xの分布関数をF(x)とするとき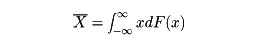

を確率変数Xの平均値という。また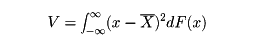

を確率変数Xの分散といい、分散の平方根を確率変数Xの標準偏差という。

［古屋　茂］

[参照項目] | 確率変数 | 数理統計

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

標準偏差 (ひょうじゅんへんさ)
standard deviation

確率・統計用語。その数値を表すのにσとかSDなどの記号が用いられる。資料x₁，x₂，……，x_nが得られたとき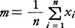が平均値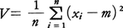，が分散で，Vの平方根が標準偏差σである。このσは資料が平均値mのまわりにどの程度の広がりで分布しているかを示す一つの尺度である。チェビシェフの不等式によれば，資料が平均値からtσ以上離れている確率は1/t²以下である。とくに分布の形がわかっている場合はもっと詳しいことが知られる。例えば正規分布に近いとき，平均値から1.95σ以上離れているものは約5%にすぎない。確率変数についても同じ趣旨で標準偏差が定義できる。Xの平均値E（X）をmとしてE｛（X－m）²｝の平方根がXの標準偏差である。Xに対しX′＝（X－m）/σをとれば，平均値が0，標準偏差が1のものに規格化される。それは尺度を統一して取り扱いたいとき，あるいは多くの確率変数を比較するときなど好つごうとなる。
→偏差値
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

標準偏差
ひょうじゅんへんさ
standard deviation

統計学の用語で，ある分布状態にある資料が，平均値のまわりにどのように散らばっているかを表わす値。一つの資料 x₁，x₂，…，x_n に対して，その平均を
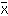＝（x₁＋x₂＋…＋x_n）÷n
で表わすとき
σ²＝｛（x₁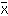－）²＋（x₂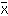－）²＋…＋（x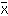_n－）²｝÷n
を，この資料の分散と呼び，その正の平方根σをこの資料の標準偏差という。正規分布の場合，平均値から標準偏差の2倍までの範囲に資料の 95.4%が入る。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

標準偏差【ひょうじゅんへんさ】

分散の平方根。σ(シグマ)で表す。資料の散らばり具合を表す重要な量で，正規分布は平均値μと標準偏差σで決まり，資料がμを中心として両側にそれぞれσ，２σ，３σ等の幅の中に出現する頻度(ひんど)は理論的に計算できる。
→関連項目確率誤差｜記述統計学｜誤差｜相関係数｜偏差

出典　株式会社平凡社

投資信託の用語集

標準偏差

データにどれだけばらつきがあるのか示す値のこと。
投資信託のリターンがどの程度ばらついているか、標準偏差を測ることで、リスクの度合いを測ることが多い。

出典　（社）投資信託協会

栄養・生化学辞典

標準偏差

　ある統計データについて，観測値間の，ばらつきの指標となる数値．分散（平均値と，各データの差の二乗の総和/（データ数−1））の平方根．

出典　朝倉書店

ブランド用語集

標準偏差

標準偏差とは、分散の平方根を取ることによって得られる、データのばらつきの大きさを示す基本統計量のことをいう。

出典　(株)トライベック・ブランド戦略研究所

世界大百科事典（旧版）内の標準偏差の言及

【確率】より

…離散形の場合なら平均値mは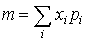，　で，分散σ²は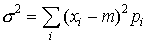，　で与えられる。分散の平方根σ(＞0)が標準偏差で散らばりの程度を表す。連続形のときも平均値，分散が類似した式で定義される。…

【誤差】より

…また多くの場合，平均値を中心にして過不足は同程度の割合で起こるとしてよいのでφ(－x)＝φ(x)と仮定する。この分布の二次のモーメント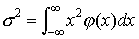，の平方根，すなわち標準偏差σは誤差論では平均誤差と呼ばれる。そしてその逆数1/σは精密さを表す。…

【散布度】より

…統計データのばらつきの度合を表す量のことを一般に散布度と呼び，分散，標準偏差，不偏分散，平均偏差，データの範囲などがある。もっともよく用いられるのは，分散，標準偏差である。…

【数理統計学】より

…代表値の近くに密集していることもあれば，両側に幅広く散らばっていることもある。この分散度を表すのに分散V，標準偏差σ，平均偏差などがある。それらはいずれもX_iととの差，すなわち偏差X_i－から求められ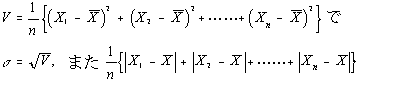，が平均偏差である。…

【積率】より

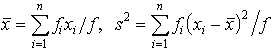…ただし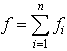，とおく。分散の平方根sを標準偏差という。aのまわりの二次の積率がもっとも小さくなるのはa＝のときである。…

※「標準偏差」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」