日本大百科全書(ニッポニカ) 「トレミーの定理」の意味・わかりやすい解説
トレミーの定理
とれみーのていり
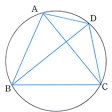
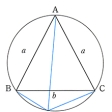
四角形が円に内接するならば、二つの対角線を二辺とする長方形の面積は、もとの四角形の二組の対辺を二辺とする二つの長方形の面積の和に等しい。これをトレミーの定理といい、この定理の逆も成り立つ。長方形は円に内接するから、長方形にトレミーの定理を適用すれば三平方の定理(ピタゴラスの定理)が現れてくる。トレミー(プトレマイオス)は150年ころアテネやアレクサンドリアで活躍した学者で古代天文学の中心人物であった。天文計算には三角比の計算が必要であるが、トレミーの仕事は『アルマゲスト』Almagestにまとめられている。トレミーの定理から、二つの弦の長さの和や差を計算する公式が導かれる。たとえば、点Aを頂点とする二等辺三角形の外接円を考え、底辺BCを弦とする弧のうち頂点Aの反対側の弧の上に任意の点Pをとると、弦PBと弦PCの長さの和は弦PAの長さに比例する。点Pが点Aのある弧の上にあれば、弦PBと弦PCの差が弦PAに比例する。
[柴田敏男]
ブリタニカ国際大百科事典 小項目事典 「トレミーの定理」の意味・わかりやすい解説
トレミーの定理
トレミーのていり
Ptolemy's theorem
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内のトレミーの定理の言及
【四辺形】より
…四辺形ABCDが円に内接すればAB・CD+BC・DA=AC・BDが成り立ち,この逆も正しい。これをトレミーの定理という。【中岡 稔】。…
※「トレミーの定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
「歓喜の歌」の合唱で知られ、聴力をほぼ失ったベートーベンが晩年に完成させた最後の交響曲。第4楽章にある合唱は人生の苦悩と喜び、全人類の兄弟愛をたたえたシラーの詩が基で欧州連合(EU)の歌にも指定され...