精選版 日本国語大辞典 「加法定理」の意味・読み・例文・類語
かほう‐ていりカハフ‥【加法定理】
改訂新版 世界大百科事典 「加法定理」の意味・わかりやすい解説
加法定理 (かほうていり)
addition theorem
(1)三角関数の最も基本的な公式に次のものがある。
(Ⅰ)sin(x+y)=sin xcosy+cosxsin y
(Ⅱ)cos(x+y)=cos x cos y-sinxsin y
(Ⅲ)tan(x+y)=\(\frac{tan x+tan y}{1-tan x tan y}\)
これらの公式を三角関数の加法定理と呼ぶ。公式(Ⅲ)はtan(x+y)をtanx,tanyの関数として表している。このように,一つの関数f(x)について,f(x+y)をf(x),f(y)の関数として表す式f(x+y)=F(f(x),f(y))をf(x)の加法定理または加法公式という。sin2x+cos2x=1だから,上の(Ⅰ)は正弦関数の,(Ⅱ)は余弦関数の加法定理といえる。一次関数kx(kは定数)の加法定理はk(x+y)=kx+ky,指数関数ekxの加法定理はek⁽x⁺y⁾=ekxe kyとなるが,逆に実数全体で定義された連続関数f(x)に対し,加法公式f(x+y)=f(x)+f(y)が成り立てばf(x)=kxとなり,加法公式f(x+y)=f(x)f(y)が成り立てばf(x)=e kxとなる。多項式F(u,v,w)に関して,F(f(x),f(y),f(x+y))=0が成り立つとき,関数f(x)は代数的加法定理をみたすという。楕円関数は代数的加法定理をみたす。
(2)排反事象,すなわちけっして同時には起こらない事象E,Fがあるとき,EまたはFのいずれかが起こる確率はEの起こる確率とFの起こる確率の和である。確率論ではこのことをp(E+F)=p(E)+p(F)と書き,確率の加法定理と呼んでいる。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「加法定理」の意味・わかりやすい解説
加法定理
かほうていり
数学において加法定理とよばれているものはいろいろあるが、ここではもっとも一般的なものとして次の二つをあげる。
(1)三角関数の加法定理 次の公式をいう。
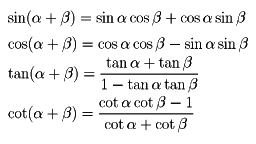
(2)確率における加法定理 k個の事象E1,E2,……, Ekがあって、このうちのどの二つも同時におこることはないとする。すなわちE1,……,Ekが排反事象であるとする。このときE1,……, Ekのうちの少なくとも一つがおこるという確率pは、各事象Eiのおこる確率p(Ei)の和に等しい。
p=p(E1)+p(E2)+……+p(Ek)
これが確率における加法定理である。この定理は古典的な確率論では次のようにして証明される。「全部でN通りの場合があって、どの場合がおこるのも同様に確からしいとする。事象Eiに対応する場合がni通りであるとするとp(Ei)=ni/Nである。一方、E1,……, Ekのうちのどの二つをとっても同時におこることはないから、これらk個のうちの少なくとも一つがおこる場合の数はN=n1+……+nkである。したがって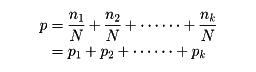
である」。確率論を公理的に構成するときは、「E1、E2が排反事象であるとき、E1、E2のうちの少なくも一方がおこる確率p(E1∪E2)は、p(E1)とp(E2)の和に等しい」という性質を確率に関する公理と考える。
[古屋 茂]
ブリタニカ国際大百科事典 小項目事典 「加法定理」の意味・わかりやすい解説
加法定理
かほうていり
addition theorem
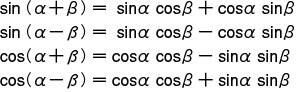 これらに対して α-β に対する公式を,減法定理ということがある。
これらに対して α-β に対する公式を,減法定理ということがある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「加法定理」の意味・わかりやすい解説
加法定理【かほうていり】
出典 株式会社平凡社百科事典マイペディアについて 情報
法則の辞典 「加法定理」の解説
加法定理【addition theorem】
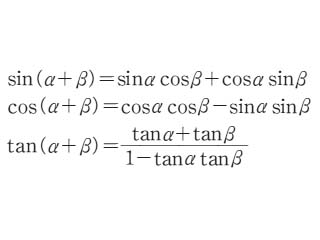
世界大百科事典(旧版)内の加法定理の言及
【三角関数】より
…三角関数は,最初は直角三角形の一つの鋭角によって定まる辺の長さの比,いわゆる三角比として定義せられ,それが一般の角に拡張された。それらに関して後述の加法定理などの性質や,別の項目で述べられる三角形の正弦定理,余弦定理が導かれ,古くから測量問題などに応用された。現代では,三角形という図形的意味とは独立に,数学の研究対象としての地位を確立し,解析学において重要な関数となっている。…
※「加法定理」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


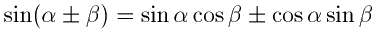
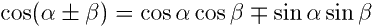
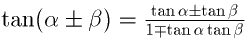 (
(