四辺形（読み）シヘンケイ（英語表記）quadrilateral

デジタル大辞泉

しへん‐けい【四辺形】

四つの辺からなる多角形。四角形。
[類語]四角・四角形・方形ほうけい・角形かくがた・升形ますがた・正方形・長方形・矩形くけい

出典　小学館

精選版 日本国語大辞典

しへん‐けい【四辺形】

〘名〙 四つの線分で囲まれた平面図形。四角形。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

四辺形 (しへんけい)
quadrilateral

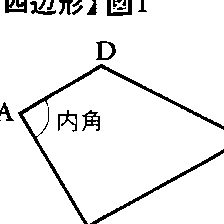
平面上に異なった4点A，B，C，Dがあって，線分AB，BC，CD，DAのどの二つの交点もA，B，C，Dのいずれかであるとき，これら4線分のつくる図形を四辺形ABCD，または四角形ABCDという。A，B，C，Dをその頂点といい，線分AB，BC，CD，DAをその辺という。四辺形によって分けられる平面の二つの部分のうちの有限の広がりをもつほうを四辺形の内部という。四辺形とその内部とを合わせた図形も四辺形と呼ばれる。四辺形の各頂点に対し，その点で交わる二つの辺が四辺形の内部においてつくる角をその頂点における内角といい，∠A，∠B，∠C，∠Dのように表す。四辺形の4内角の和は4直角である。どの内角も2直角を超えない四辺形を凸四辺形といい（図1），そうでない四辺形を凹四辺形という（図2）。四辺形ABCDにおいて，∠Aと∠C，∠Bと∠Dを対角といい，辺ABと辺CD，辺BCと辺DAを対辺という。また，線分AC，BDを対角線という。凸四辺形では対角線は四辺形の内部にあるが，凹四辺形ではそうとは限らない。2組の対辺がそれぞれ平行である四辺形を平行四辺形といい，頂点がA，B，C，Dである平行四辺形を▱ABCDで表す（図3）。平行四辺形とは，また，2組の対角の大きさがそれぞれ等しい四辺形，2組の対辺の長さがそれぞれ等しい四辺形，あるいは2組の対角線が互いに他を2等分する四辺形ということができる。4辺の長さがすべて等しい四辺形を菱形といい（図4），4内角がすべて等しい四辺形を長方形，または矩形という（図5）。菱形では二つの対角線が直角に交わり，長方形では二つの対角線の長さは等しい。菱形で同時に長方形である四辺形を正方形，または正四角形という（図6）。1組の対辺だけが平行で，もう1組の対辺が平行でない四辺形を台形，または梯形という（図7）。四辺形のすべての頂点を通る円があるとき，四辺形は円に内接するといい，この円を四辺形の外接円という（図8）。また四辺形のすべての辺に接する円があるとき，四辺形は円に外接するといい，この円を四辺形の内接円という（図9）。四辺形が円に内接するための条件は対角の和が2直角になることであり，四辺形が円に外接するための条件は2組の対辺の長さの和が等しくなることである。四辺形ABCDが円に内接すればAB・CD＋BC・DA＝AC・BDが成り立ち，この逆も正しい。これをトレミーの定理という。
執筆者：中岡 稔

図1～図9

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

四辺形
しへんけい

→四角形

出典　小学館　日本大百科全書(ニッポニカ)