パスカルの定理
ぱすかるのていり
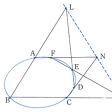
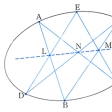
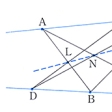
平面上の6点が同一の二次曲線上にあるための必要十分条件は、これらの点を頂点とする六角形の三組の対辺の交点が一直線上にあることである。この定理をパスカルの定理という。ここで、六角形は普通の意味の多角形である必要はない。図Aは楕円(だえん)についてパスカルの定理を描いてあるが、図Bのような六角形ABCDEFでもよい。この場合、六つの辺のうちABとDE、BCとEF、CDとFAがそれぞれ対辺である。図Cは二次曲線が退化して二直線になった場合で、パップスの定理ともよばれている。
パスカルの定理を用いると、5点A、B、C、D、Eが与えられたとき、それらを通る二次曲線を作図することができる。実際、図Bで直線AFをAを通る任意の直線と考え、与えられた5点から図に従ってL、次にN、次に直線LN、次にM、次に二直線AF、EMの交点としてFを求めれば、Fの軌跡が求める二次曲線である。この定理を用いて二次曲線が作図できることからわかるように、パスカルの定理は二次曲線の定義と同等といってよいほど重要な射影幾何学の定理である。
［立花俊一］
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
パスカルの定理 (パスカルのていり)
Pascal's theorem
〈3点A，C，Eが1直線上にあり，3点B，D，Fが他の1直線上にあるとき，ABとDE，BCとEF，CDとFAの交点は1直線上にある〉（図1）という定理，およびその一般化である〈二次曲線上に6点A，B，C，D，E，Fがあるとき，ABとDE，BCとEF，CDとFAの交点は1直線上にある〉（図2）という定理をパスカルの定理という。これはB.パスカルが16歳のときに発見したといわれ，射影幾何学の重要な定理の一つである。パスカルの定理に双対な次の定理はブリアンションC.J.Brianchonの定理と呼ばれている。〈二次曲線に六つの接線a，b，c，d，e，fが引かれているとき，a，bの交点とd，eの交点を結ぶ直線，b，cの交点とe，fの交点を結ぶ直線，c，dの交点とf，aの交点を結ぶ直線は1点で交わる〉（図3）。
執筆者：中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
パスカルの定理
パスカルのていり
Pascal's theorem
円錐曲線に内接する六角形 ABCDEFの相対する辺 ABと DE，BCと EF，CDと FA，またはその延長の交点P，Q，Rは1直線上にあるという定理。その後の射影幾何学に重要な役割を演じた。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典
「パスカルの定理」の解説
パスカルの定理【Pascal's theorem】
円錐曲線に内接する単純六角形の3組の対辺の交点は同一直線上に存在する．
出典 朝倉書店法則の辞典について 情報
世界大百科事典（旧版）内のパスカルの定理の言及
【幾何学】より
…デザルグやパスカルは，無限遠点やそれらの集りである無限遠直線を考えれば，ギリシア人が個々別々に陳述し証明した事柄が，統一的，かつ普遍的に得られることをいろいろな例によって示した。これらの中に，〈二つの三角形の対応する3頂点を結ぶ直線が1点で交われば，対応する辺の交点は1直線上にあり，この逆も成り立つ〉というデザルグの定理や，〈円錐曲線に内接する六角形の相対する辺，またはその延長の交点は1直線上にある〉というパスカルの定理がある。デザルグやパスカル以後は，解析幾何学や微積分学の華々しい進展の陰に隠れて，射影的方法による幾何学の研究は忘れられていたが，18世紀末にG.モンジュによって透視図法が復活されたのをきっかけとして，19世紀前半には射影的方法による幾何学の組織的研究が行われ，射影幾何学と呼ばれる数学の一分科が成立した。…
【射影幾何学】より
…このようなわけで，直線図形ばかりでなく，円錐曲線も射影幾何学の対象となる。これに関し，〈円錐曲線に内接する六角形の相対する辺の交わりである3点は共線である〉というパスカルの定理(図4)，〈円錐曲線に外接する六角形の相対する頂点を結ぶ3直線は共点である〉というブリアンションの定理(図5)は有名である。射影平面上では，通常の平面上のときと同じく，〈異なる2点と結合する直線がつねに一つ定まる〉が，通常の平面上のときと違って平行線はなく，〈異なる2直線と結合する点がつねに一つ定まる〉。…
【パスカル】より
…早く妻を亡くしたエティエンヌは，1631年官を辞して一家でパリに赴き，[メルセンヌ]の主宰する科学アカデミーに出入りするかたわら，子どもの教育に専念する。息子のパスカルは早熟の天才でとくに数学に才覚をあらわし，早くから父とともに科学者の集りに出席したが，16歳のときに[デザルグ]の影響の濃い《円錐曲線試論》を発表(1640)し，射影幾何学における〈[パスカルの定理]〉を明らかにした。40年再び官についたエティエンヌとともに一家はルーアンに移る。…
※「パスカルの定理」について言及している用語解説の一部を掲載しています。
出典｜株式会社平凡社「世界大百科事典（旧版）」
