二次曲線（読み）ニジキョクセン（英語表記）quadratic curve

デジタル大辞泉

にじ‐きょくせん【二次曲線】

二次方程式によって表される曲線。放物線・楕円・双曲線の総称。→円錐曲線

出典　小学館

精選版 日本国語大辞典

にじ‐きょくせん【二次曲線】

1. 〘 名詞 〙 二元二次方程式によって表わされる平面図形の総称。係数の値のとり方によって、円、楕円、双曲線、放物線、二直線などになる。円錐曲線。〔電気工学ポケットブック（1928）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

二次曲線 (にじきょくせん)
quadratic curve

平面上の直交座標（x，y）を用いて，実数係数の二次方程式，

　Ax²＋2Hxy＋By²＋2Gx＋2Fy＋C　　　＝0

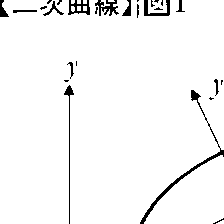
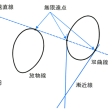
で表される曲線を総称して二次曲線という。係数A，B，……，Hのとりようによっては，方程式を満たす点がまったく存在しなかったり（例えばx²＋y²＋1＝0），ただ1点にすぎなかったり（例えばx²＋y²＝0）することもあるし，また方程式は一つの直線を表したり（例えばx²＋2xy＋y²＝0），二つの直線を表したり（例えばx²－y²＝0）することもある。このようにならない二次曲線を固有な二次曲線という。固有な二次曲線はAB－H²が正であるか，負であるか，0であるかに応じて，適当な直交座標（x′，y′）を用いることにより，（x′/a）²＋（y′/b）²＝1，（x′/a）²－（y′/b）²＝1，y′²＝4ax′と表され，楕円，双曲線，放物線となる（図1）。したがって固有な二次曲線は円錐曲線，すなわち直円錐面をその頂点を通らない平面で切ったときの切口として現れる曲線にほかならない（図2）。固有な二次曲線は，また，平面上で1定点と1定直線からの距離の比が一定な点の描く図形ともいえる。この定点を焦点，定直線を準線といい，一定な比の値を離心率という。離心率が1より小さいか，1より大きいか，1に等しいかに応じて，曲線は楕円，双曲線，放物線になる。さらに，固有な二次曲線は射影的関係にある二つの線束の対応する直線の交点の作る図形であるともいえるし（図3），射影的関係にある二つの点列の対応点を結ぶ直線の描く図形であるともいえる（図4）。
執筆者：中岡 稔

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

二次曲線
にじきょくせん
quadratic curve

平面上で二次方程式
　　ax²+2hxy+by²+2gx+2fy+c=0
の解(x,y)全体がつくる図形をいう。たとえば
　　5x²+4xy+2y²+2x+4y+2=0
は、適当な直交座標系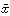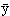｛,｝によって書き直せば6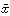²+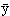²=3となるから楕円(だえん)である。また、
　　a=b=c=1, h=g=f=0
である二次曲線はx²+y²=-1であるから実数解をもたない。この方程式が表す曲線を虚円というが、円は楕円の仲間であるから、虚楕円の一つである。二次曲線の式が因数分解して、たとえば
　　(x-y+2)(x+2y+1)=0
のようになれば、この二次曲線はx-y+2=0なる直線とx+2y+1=0なる直線に分解する。一般に、二次曲線は二直線に分解する場合と分解しない場合がある。分解しない場合は
　　h²-ab＞0,=0,＜0
に応じて、双曲線、放物線、実または虚の楕円になり、これらの曲線は円錐曲線(えんすいきょくせん)、または固有二次曲線と総称される。

　二次曲線の式を斉次(せいじ)座標x=X/Z,y=Y/Zで表せば
　　aX²+bY²+cZ²+2fYZ+2gZX+2hXY=0
となり、無限遠直線Z=0との交点は、
　　aX²+2hXY+bY²=0
により求められる点(X,Y,0)である。したがって、判別式h²-abの正、ゼロ、負に応じて、双曲線は無限遠直線と2点で交わる、放物線は接している、楕円は交わらない、ことがわかる。これが円錐曲線の無限遠直線を用いた特徴づけである。二次曲線がある点に関して対称であるとき、この点を、考える二次曲線の中心という。中心がただ一つの二次曲線を有心、それ以外のとき無心という。楕円、双曲線、交わる二直線の場合は有心であり、放物線、平行二直線は無心である。

［立花俊一］

二次曲線

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

二次曲線
にじきょくせん
quadratic curve

平面上で，座標 P（x，y）が，2次方程式 ax²＋2kxy＋by²＋2fx＋2gy＋c＝0 を満足するような点 P全体は，二次曲線と呼ばれる図形をつくる。ここに係数 a，k，b，f，g，c は任意の実数である。ただし，複素変数で考えて，係数にも複素数を許した複素二次曲線を考えることもある。二次曲線は係数の値の取り方によって，放物線，楕円，双曲線（これらを固有二次曲線という），1点，1直線，2直線（これらを退化した二次曲線という）などの図形になる。すべての固有二次曲線は，方程式 y²＝2px－（1－q²）x² （p＞0）の形に書き直すことができ，これを二次曲線の頂点方程式という。方程式からも明らかなように，この場合，x軸は二次曲線の主軸となり，y軸は二次曲線の一つの接線となる。この p を二次曲線のパラメータ，q を離心率という。また原点は曲線の頂点の一つである。離心率によって二次曲線を分類すれば，

ｑ＝0 のとき		半径p の円
ｑ＜1 のとき		楕円
ｑ＝1 のとき		放物線
ｑ＞1 のとき		双曲線

となる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

二次曲線【にじきょくせん】

平面上で直角座標x，yの二次方程式ax²＋２hxy＋by²＋２gx＋２fy＋c＝０をみたす点（x，y）の全体。係数から作った行列式（式１）を判別式といい，D＝abc＋２fgh−bf²−ag²＋ch²である。ここでD≠０なら固有二次曲線（楕円・放物線・双曲線，つまり円錐曲線）になり，D＝０なら式が因数分解されて二つの直線になる。→二次関数／二次曲面
→関連項目楕円

出典　株式会社平凡社