円錐曲線（読み）エンスイキョクセン

デジタル大辞泉

えんすい‐きょくせん〔ヱンスイ‐〕【円^×錐曲線】

直円錐の円錐面を、頂点を通らない平面で切ったときの切り口の平面曲線。切る傾きによって、円・楕円・双曲線・放物線ができる。二次方程式が円錐曲線に対応するところから、二次曲線ともいう。

出典　小学館

精選版 日本国語大辞典

えんすい‐きょくせんヱンスイ‥【円錐曲線】

1. 〘 名詞 〙 直円錐の表面を平面で切ったときできる切り口の曲線。切り方によって円、楕円、放物線、双曲線、二直線などになる。これを平面上に描けば、座標ｘ、ｙの二次方程式で表わされるので二次曲線ともいう。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

円錐曲線
えんすいきょくせん

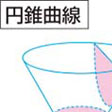
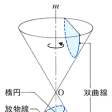
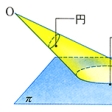
直円錐を頂点を通らない平面で切ったときの切り口の平面曲線の総称。空間の1点Oで交わる直線mとlがある。直線mを軸として直線lを1回転するとき、直線l（母線）は、点O（頂点）の上下に二つの直円錐を描く。これを切る平面の傾きによって、楕円(だえん)、放物線または双曲線ができる。切る平面が母線に平行なときは放物線になる。母線に平行でないときは、切り口が円錐面の一方だけにあれば楕円、上下両方に現れれば双曲線である。円錐の軸mに垂直な平面で切った切り口の曲線は円であるから、円は楕円の特別なものと考えられる。点Oを光源と考えれば、光源から発する光を円で遮ったときのそれぞれの切断平面上の影が楕円、放物線、双曲線ということでもある。この意味から射影幾何学では、これら3種の曲線は互いに区別できない、すなわち「互いに射影的に合同」としている。直円錐の切り口としての楕円、放物線、双曲線は、紀元前300年ころのギリシアですでに知られていた。とくにアポロニウスは『円錐曲線論』8巻を著し、これら3種の曲線に共通な性質を詳しく調べている。

　その後、時代がずっと下って、フランスの数学者パスカルは円錐曲線を射影幾何学の立場から研究し大きな貢献をした。17世紀に解析幾何学が導入されてからは、円錐曲線はx、yの二次方程式の解がつくる集合として二次曲線であることがわかり、解析的立場からも研究されるようになった。

［立花俊一］

[参照項目] | 二次曲線

円錐曲線（上下二つの直円錐を切る平面）

円錐曲線（光源から発する光を円で遮った…

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

円錐曲線【えんすいきょくせん】

直交しない相交わる２直線の一方を軸に回転させたときにできる円錐を頂点を通らない平面で切った切口の曲線の総称。母線に平行でない平面で切るとき，切口が頂点の一方側だけにできれば楕円（円を含む），両側にできれば双曲線，母線の一つに平行な平面で切れば放物線となる。円錐曲線は一定点（焦点）と一定直線（準線）までの距離の比（離心率）が一定な点の軌跡であり，離心率が１より小さければ楕円，大きければ双曲線，１に等しければ放物線になる。→二次曲線／アポロニオス（ペルゲの）
→関連項目回転体｜曲線

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

円錐曲線
えんすいきょくせん
conic section

円錐切断曲線ともいう。直円錐を，頂点を含まない平面で切取った切り口の平面曲線は，楕円，双曲線，放物線のいずれかである。これらを円錐曲線という。以上の3つの曲線は二次曲線でもある。アポロニオスによる円錐曲線の計量的研究は，古代における偉大な数学的業績である。 B.パスカルも 16歳のとき「円錐曲線試論」を書き，パスカルの定理「円錐曲線に内接する6辺形の3組の対辺の交点は，一直線上にある」を述べ，G.デザルグの射影的方法の有効性を認めた。射影幾何学では，初め円錐曲線が重要な研究対象であった。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

円錐曲線 (えんすいきょくせん)

→二次曲線

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の円錐曲線の言及

【円錐】より

…円錐面とその頂点を通らない平面との交線としてできる曲線は楕円(円を含む)，双曲線，放物線の3種である。この理由で，これらの曲線は円錐曲線(二次曲線)と総称される。【中岡 稔】。…

【二次曲線】より

…固有な二次曲線はAB－H²が正であるか，負であるか，0であるかに応じて，適当な直交座標(x′，y′)を用いることにより，(x′/a)²＋(y′/b)²＝1，(x′/a)²－(y′/b)²＝1,y′²＝4ax′と表され，楕円，双曲線，放物線となる(図1)。したがって固有な二次曲線は円錐曲線，すなわち直円錐面をその頂点を通らない平面で切ったときの切口として現れる曲線にほかならない(図2)。固有な二次曲線は，また，平面上で1定点と1定直線からの距離の比が一定な点の描く図形ともいえる。…

※「円錐曲線」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」