リーマン積分
りーまんせきぶん
Riemann integral
ドイツの数学者リーマンの与えた定義による積分の方法。
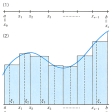
f(x)は、区間[a,b]で与えられた有界な関数であるとする。さらに、区間[a,b]を分点x1,x2,……,xn-1(x0=a,xn=bとする)によって細分し、その分割をΔとする(図の(1))。そして、各小区間内に一点ξk(xk-1≦ξk≦xk)を任意にとり、次の和S(Δ)を考える。
S(Δ)=f(ξ1)(x1-x0)+f(ξ2)
(x2-x1)+……+f(ξn)(xn-xn-1)
(図の(2)の長方形の面積の和)
そして、どのように分割Δをとり、またどのように点ξkを各小区間から選んでも、分割Δを構成する小区間の幅を一様に小さくしていけば(すなわちxk-xk-1(k=1,2,……,n)の最大のものを0に近づける、このときもちろんn→∞)、S(Δ)がある一定の値Iに近づくとき、f(x)はリーマン積分可能であるといい、
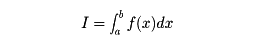
で表す。
リーマンはこの定義を与えたのち、単調関数はリーマン積分可能であることを示した(1854)。連続関数がリーマン積分可能であることを示したのは、ハイネである(1874)。
[竹之内脩]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
リーマン積分 (リーマンせきぶん)
Riemann integral
積分の概念は微分とともに17世紀後半にI.ニュートンとG.W.F.ライプニッツによって発見されたが,これを現代数学の立場で,一般的な形に厳密に定義したのがリーマン積分である。19世紀に入ってA.L.コーシーやP.G.L.ディリクレにより関数の概念が見直され,その意味が確立されたことにより,積分の概念もG.F.B.リーマンにより次のように一般的に定義されるに至った。
区間a≦x≦bで定義された有界な実数値関数f(x)があるとき,この区間の分割,
⊿:a=x0<x1<x2<……<xn-1<xn=b
を考え,各小区間xj-1≦x≦xj(j=1,……,n)に属する任意の点ξjをとり,分割⊿と点の組ξ={ξj}によって定まる和,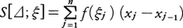 を考える。小区間の長さの最大のものが0に近づくように,分割を限りなく細かくしていくとき,S[⊿;ξ]の値が分割⊿や点の組ξの列のとり方に無関係な一定の値Sに近づくならば,f(x)は区間a≦x≦bでリーマン積分可能または単に積分可能であるといい,
を考える。小区間の長さの最大のものが0に近づくように,分割を限りなく細かくしていくとき,S[⊿;ξ]の値が分割⊿や点の組ξの列のとり方に無関係な一定の値Sに近づくならば,f(x)は区間a≦x≦bでリーマン積分可能または単に積分可能であるといい,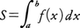 と書いて,これをf(x)のaからbまでの積分という。連続関数の積分は微分の逆演算である。積分概念をさらに発展させたものとして,20世紀初めにH.ルベーグによって創始されたルベーグ積分がある。
と書いて,これをf(x)のaからbまでの積分という。連続関数の積分は微分の逆演算である。積分概念をさらに発展させたものとして,20世紀初めにH.ルベーグによって創始されたルベーグ積分がある。
→積分 →ルベーグ積分
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
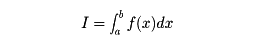


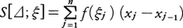 を考える。小区間の長さの最大のものが0に近づくように,分割を限りなく細かくしていくとき,S[⊿;ξ]の値が分割⊿や点の組ξの列のとり方に無関係な一定の値Sに近づくならば,f(x)は区間a≦x≦bでリーマン積分可能または単に積分可能であるといい,
を考える。小区間の長さの最大のものが0に近づくように,分割を限りなく細かくしていくとき,S[⊿;ξ]の値が分割⊿や点の組ξの列のとり方に無関係な一定の値Sに近づくならば,f(x)は区間a≦x≦bでリーマン積分可能または単に積分可能であるといい,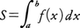 と書いて,これをf(x)のaからbまでの積分という。連続関数の積分は微分の逆演算である。積分概念をさらに発展させたものとして,20世紀初めにH.
と書いて,これをf(x)のaからbまでの積分という。連続関数の積分は微分の逆演算である。積分概念をさらに発展させたものとして,20世紀初めにH.