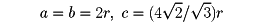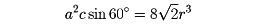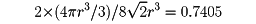六方最密充填（読み）ろっぽうさいみつじゅうてん（英語表記）hexagonal closest packing

精選版 日本国語大辞典

ろっぽう‐さいみつじゅうてんロクハウ‥【六方最密充填】

1. 〘 名詞 〙 最密充填構造の一つ。同じ大きさの球の列を重ねるとき、一層目のすきまの上にはまるように二層目を置き、三層目が初層の真上にくるもの。各球の中心を格子点とすると六方晶系の格子となる。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

六方最密充填
ろっぽうさいみつじゅうてん
hexagonal closest packing

同寸法剛体球の三次元最密充填の一種。剛体球の二次元最密配列を積み上げる際に、第三層を第一層の真上に置くと得られる構造である。各球の中心を格子点とする格子構造が六方格子となるところから六方最密充填という。球の半径をrとすると、単位格子は

の六方格子となり、その体積

の中に正味2個の球があるので、充填率は

となって、立方最密充填の場合とまったく同じになる。

［岩本振武　2015年8月19日］

[参照項目] | 結晶 | 立方最密充填

六方最密充填

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の六方最密充填の言及

【最密充てん(最密充塡)】より

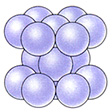
…したがって，球の最密充てんの並べ方は，積層順を示すA,B,Cの積み重ね方で表現できる。ABの繰返しで表されるものは，ACのそれと同じ型式になり，六方晶系の格子がつくられるので，この様式を六方最密充てん構造hexagonal closest packing of spheres(hcpと略す)という。またABC(またはACB)の繰返しの積み重ね方は，層に垂直な方向を対角線とする面心立方格子の構造となるので，この様式を，立方最密充てん構造cubic closest packing of spheres(ccpと略す)という。…

※「六方最密充填」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」