変換群（読み）へんかんぐん

日本大百科全書(ニッポニカ)

変換群
へんかんぐん

平面の原点の周りの回転移動は平面を自分自身の上に一対一に写す写像であり、その全体は群をなしている。変換群はこれを次のようにして一般化したものである。まず、Mを集合とするとき、Mを自分自身の上に一対一に写す写像をMの変換という。σ、τをMの変換とするとき、変換τに引き続いて変換σを行った結果もまたMの変換になるから、これをσとτの積という。Mの変換の一つの集まりGがこの積に関して群をなすとき、GをMに働く変換群という。Mに働く変換群として、Mのなかで意味をもつなにかある概念を変えないようなMの変換の全体という形をとることが多い。たとえば、Mが平面のとき、任意の2点間の距離を変えないような変換の全体として合同変換群がある。あるいは、内積を変えないような変換の全体として直交（変換）群がある。また、Mがベクトル空間のとき、ベクトル和とスカラー倍を変えないような変換の全体として一般線形変換群がある。

［高木亮一］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

変換群
へんかんぐん
group of transformations

ある空間の上の点変換の集合がある場合，2つの変換を引続いて行うことを2つの変換の結合と考えるとき，これらの変換の集合がこの結合法に関して群をつくるならば，これを変換群という。たとえば直交軸の設定された平面上では，原点のまわりの角 θ の回転は，方程式
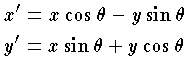で表わされるが，これらの回転の集合は上の意味で群をつくる。この変換群を回転群と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典