二次形式（読み）にじけいしき（英語表記）quadratic form

改訂新版　世界大百科事典

二次形式 (にじけいしき)
quadratic form

x₁²＋4x₁x₂＋x₂²＝x₁²＋2x₁x₂＋2x₂x₁＋x₂²のように，いくつかの変数x₁，x₂，……，x_nの多項式で，すべての項が二次の項だけからなるものをx₁，x₂，……，x_nについての二次形式という。二次形式は対称行列（S＝^tSを満たす行列。ここで^tSはSの転置行列）を用いて，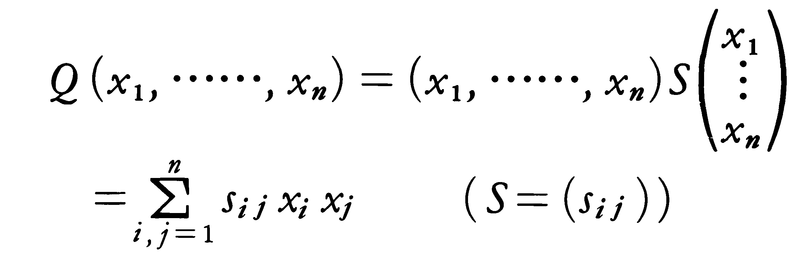

と表される。上の例では，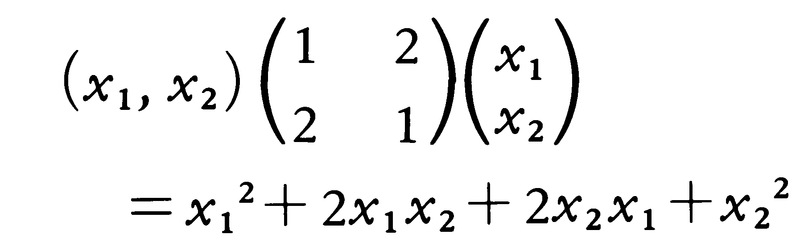

である。QのことをSで決まる二次形式という。以下，（x₁，……，x_n）＝xと略記することにする。二次形式Qに対し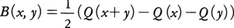，をQの極形式という。Qは，Bを用いてQ（x）＝B（x，x）と表される。Sの行列としての階数rをQの階数といい，Sが正則のときQは非退化であるという。これは，すべてのyに対してB（x，y）＝0となるxは0に限るということもできる。

　二次形式に適当な直交変換を行うことにより，

　α₁x₁′²＋……＋α_px_p′²－α_p+1x_p+1′²－

　　……－α_p+qx_p+q′²　（α₁＞0）　

という形にできる。このときp＋q＝r（rは階数）で，この（p，q）を二次形式の符号数といい，この形に変換することをQを主軸変換するという。

　二次形式において，すべてのxに対してQ（x）≧0で，Q（x）＝0となるのはx＝0に限るとき正値形式といい，Q（x）≦0でQ（x）＝0ならば，x＝0であるとき負値形式であるという。これ以外のときは不定値形式であるという。この三つの場合は，符号数を用いて（p，q）＝（n，0），（0，n），それ以外と区別できる。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

2次形式
にじけいしき
quadratic form

たとえば f(x)＝ax²－2kxy＋by² は，変数 x，y についての2次の同次式であるから，このような場合を2変数の2次形式という。一般に，x₁，x₂，…，x_n を n 個の変数とした2次の同次多項式
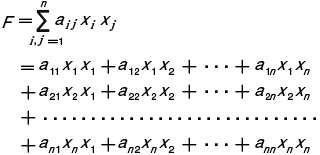があるとき，これを x₁，x₂，…，x_n の2次形式という。上の式 F の右辺の係数からつくられる対称行列
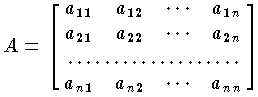を，2次形式 F の行列という。このように2次形式と対称行列とは密接な関係をもっており，2次形式 F は，対称行列 A と2つのベクトル
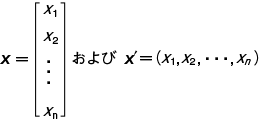によって F＝x'Ax と表わすこともできる。 a_ij および x_i がともにすべて実数であれば実2次形式，またそれらがともにすべて複素数であれば複素2次形式という。

出典　ブリタニカ国際大百科事典 小項目事典