関数解析学（読み）かんすうかいせきがく（英語表記）functional analysis

改訂新版　世界大百科事典

関数解析学 (かんすうかいせきがく)
functional analysis

19世紀の終りごろまでは，関数はおもにその各点における値に着目して研究されてきたが，20世紀に入って集合論の発祥とともに，ある条件を満たす関数全体の集り（集合）を考え，個々の関数をその集合の要素として扱う考え方が行われるようになった。そうして，ふつうのユークリッド空間でベクトルの加法や定数倍の算法を考えたり，点列がある1点に近づくという〈収束〉の概念を用いたりするのと同様に，関数の集合の中でベクトルの算法や収束を考える。例えば閉区間［a，b］の上で連続な関数の全体をCと書くことにすると，連続関数の和や定数倍は連続関数であるから，Cはベクトル空間の性質をもっている。また連続関数の列の一様収束の極限は連続関数であるから，Cにおける収束とは関数列の一様収束のことであると約束することにより，ふつうのユークリッド空間における点列の収束と同様な取扱いができる。さらに，関数を微分する操作や積分する操作を関数から関数への対応と考え，このような対応を作用素，または演算子という。このようにベクトル算法と収束概念の定義された空間の構造や，その空間における作用素の性質を一般的に調べることにより，従来は別個のものと考えられてそれぞれの方法で取り扱われていたいくつかの理論が，統一された簡単な方法で，より一般的に扱われるようになり，また他方において，多くの新しい事実を導くことができるようになった。こうして現代化された解析学の基礎となる部門が関数解析であり，その理論の代表として，20世紀前期に創始されたヒルベルト空間論，バナッハ空間論，20世紀中期に創始された超関数論があげられる。このうち，バナッハ空間論とヒルベルト空間論の概略について以下に述べるが，〈バナッハ空間〉〈ヒルベルト空間〉の定義や例は，それぞれの項目を参照されたい。また超関数論については〈超関数〉の項目を参照されたい。

バナッハ空間論

バナッハ空間Xからバナッハ空間Yの中への作用素Tが，

　T（αx＋βy）＝αTx＋βTy

　　　　　　（x，y∈X;α，βは複素数）

を満たすとき，Tを線形作用素という。また正数γが存在して／Tx／≦γ／Tx／が成り立つときTは有界であるといい，このようなγの下限を／T／と書いて，作用素Tのノルムnormという。線形作用素Tが連続，すなわち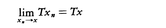，を満たすこととTが有界なこととは同等である。前に述べた作用素の定義で，とくにYが複素数体のとき，その作用素のことを汎関数という。

共役空間，共役作用素

Xの上の有界線形汎関数fの全体は，

　（f＋g）（x）＝f（x）＋g（x）

　（αf）（x）＝αf（x）

なるベクトル演算と汎関数ノルム／f／によってバナッハ空間になる。これをX^＊と書き，Xの共役空間という。例えば，1＜p＜∞のとき1/p＋1/q＝1になるqをとると，L_p（a，b）^＊は次の意味においてL_q（a，b）になる:各f∈L_p（a，b）^＊に対しY_f∈L_q（a，b）が1対1に対応して，任意のx∈L_p（a，b）に対して，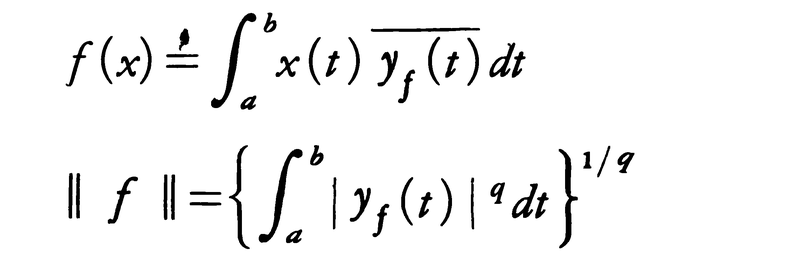

である。とくにXがヒルベルト空間ならばX^＊＝Xとなる。また，TがXからYの中への有界線形作用素のとき，f（Tx）＝（T^＊f）（x）により，Y^＊からX^＊の中への有界線形作用素T^＊が定義されて／T^＊／＝／T／となる。このT^＊をTの共役作用素という。線形作用素は有次元ベクトル空間に作用する行列に相当するものであり，TからT^＊を作る操作は，行列（a_ij）から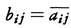なる行列（b_ij）を作り出す操作に相当する。

ハーン=バナッハの拡張定理Harn-Banach extension theorem

Xの線形部分空間Mがあって，ノルムから定義される距離に関して閉集合であるとする。このとき，Mで定義された有界線形汎関数f₀は，X全体で定義された有界線形汎関数fに拡張され，／f／＝／f₀／となる。この拡張定理を使って，古典統計力学の数学的基礎づけとしてのエルゴート定理などが得られる。

積分方程式への応用

バナッハ空間Xからバナッハ空間Yの中への作用素Tが，Xの有界集合をYのコンパクト集合に写す対応をするとき，Tは完全連続であるという。XからXの中への完全連続作用素Tと，u∈Xおよび定数λ≠0が与えられたとき，x∈Xに関する方程式，

　λx－Tx＝0　　　　　　　……（1）

　λx－Tx＝u　　　　　　 ……（2）

に対して次の（1）（2）のいずれかが成立する。（1）（1）が0以外の解xをもたない場合は，（2）は任意のu∈Xに対して唯一つの解xをもつ。（2）（1）が0以外の解xをもつ場合は，その解の中で線形独立なものは有限個であり，そのとき（2）が解をもつための条件は，λf－T^＊f＝0なる任意のf∈X^＊に対してf（u）＝0なることである。これは，リース=シャウダーの択一定理と呼ばれ，積分方程式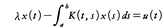，にあてはめると，すなわち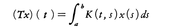，なる作用素Tを考えると，フレドホルムの択一定理が得られる。

非線形問題

常微分方程式の初期値問題，

　x′＝f（t，x），x（0）＝a ……（3）

は，未知関数x（t）に関する積分方程式，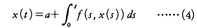

と同等である。（4）の解は連続関数x（t）に連続関数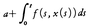を対応させる作用素の不動点である。この考えによりG.D.バーコフとケロッグO.D.Kellog（1878-1932）は，微分方程式の解の存在を，バナッハ空間における（必ずしも線形でない）完全連続作用素の不動点定理として証明した。このような考え方は，シャウダーJ.P.Schauder（1899-1943），ルレーJ.Leray（1906-98）らによって，偏微分方程式の解の存在証明にも拡張された。

線形作用素の半群

バナッハ空間XからXへの有界線形作用素の族｛T_t｜t≧0｝があって，（1）T_tT_s＝T_t+s（半群性），（2）T₀＝I（恒等作用素），（3）任意のx∈Xに対して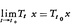（連続性）を満たすとき，｛T_t｜t≧0｝を1パラメーター半群または単に半群と呼ぶ。また，次の式の右辺の極限が存在するようなx∈Xに対して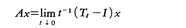，で定義される線形作用素Aを，半群｛T_t｝の生成作用素という。生成作用素は一般には有界でない作用素である。1948年に吉田耕作とヒレE.Hille（1894-1980）は，互いに独立に半群の生成作用素の特徴づけを行うことにより，半群の理論を確立した。これは吉田=ヒレの理論と呼ばれ，偏微分方程式や確率過程などに応用が広く，それらの理論の発展にたいへんに役だっている。

ヒルベルト空間論

ヒルベルト空間Xにおける内積を（x，y）と書く。Xの部分集合，

　S＝｛e₁，e₂，……，e_k，……｝

が／e_k／＝1，j≠kならば（e_j，e_k）＝0を満たすとき，正規直交系という。とくに，すべてのkに対して（x，e_k）＝0となるx∈Xは0に限るとき，Sは完全であるという。Sが完全正規直交系ならば，任意のx∈Xは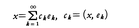，と展開され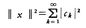，となる。

　ヒルベルト空間はバナッハ空間でもあり，したがって，バナッハ空間について前に述べたことはすべて成立するから，それ以外の事項を以下に述べる。線形作用素，線形汎関数や，それらの有界性などの意味は，前にバナッハ空間に関する事項として述べたとおりである。

射影作用素，リースの定理

MがXの閉線形部分空間ならば，任意のx∈Xはx＝y＋z（y∈M，zはMのすべての元と直交）と一意的に分解され，したがってy＝Pxなる有界線形作用素Pが定まる。このPをXからMへの射影作用素という。射影作用素PはP²＝P（べき等性）を満たし，また任意のx，y∈Xに対して（Px，y）＝（x，Py）（対称性）となる。逆に，有界線形作用素Pがべき等性と対称性を満たせば，PはXのある閉線形部分空間への射影作用素である。X上の任意の有界線形汎関数fに対してy_f∈Xが一意的に定まってf（x）＝（x，y_f）となる。この意味でXの共役空間X^＊はXと同じと考える。

ヒルベルト空間におけるスペクトル理論

弦や膜のような連続的な媒質の振動を数学的に定式化すると，微分方程式の境界値問題になる。例えば，両端ξ＝0，ξ＝1を固定した密度一定な弦の振動は，境界値問題，

　x″＝－μ²x，x（0）＝x（1）＝0　　　……（5）

になる。これがx（ξ）0なる解をもつようなμが固有振動数である。このようなμ²を固有値といい，これに対応する解x（ξ）0をこの固有値に属する固有関数という。この境界値問題は，〈グリーン関数〉と呼ばれるところの関数，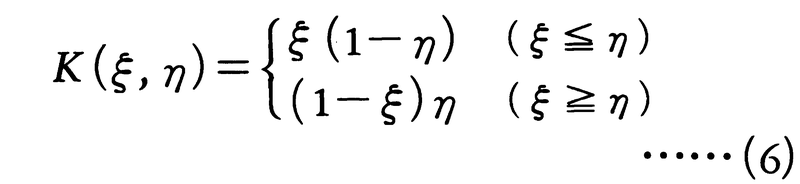

を用いて次の積分方程式に転換される。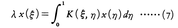

　　（ただしλ＝μ⁻²。積分方程式（7）では，このλのことを固有値という）

　このK（ξ，η）により関数x∈L₂（0，1）（これはヒルベルト空間である）を関数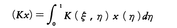，に写す作用素Kを考えると，Kは有界線形作用素であり，また関数K（ξ，η）の対称性，K（ξ，η）＝K（η，ξ）から，作用素Kの対称性，

　（Kx，y）＝（x，Ky）　　　　……（8）

　　　　　　　（なお（　，）は内積を示す）

が出る。さらにKは完全連続であり，

（7）は，

　Kx－λx＝0　　　　　　　……（9）

と書ける。一般に，K（ξ，η）が0≦ξ，η≦1で連続のとき，積分方程式（7）の固有値λはたかだか可算無限個で，0にのみ集積する。それらをλ₁，λ₂，……とすると，各λ_iに属する固有ベクトルは有限次元空間M_i（それをλ_iに属する固有空間という）を張り，i≠jならばM_iとM_jは直交する。X＝L₂（0，1）からM_iへの射影作用素をP_iとすると，任意のx∈Xに対して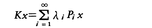，　　（右辺の無限級数はノルムに関して収束）

となる。このことを，

と書き表す。以上のことは一般のヒルベルト空間Xにおける完全連続対称線形作用素Kに対する方程式（9）について成立する。任意の実数λに対して，λ_i≦λなるすべてのiについて加えることを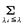と書くことにして，

と定義すると，λ＞μならば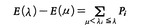，となる。だから，実数直線を，

　－∞＜ξ₀＜ξ₁＜……＜ξ_k＜……＜ξ_n＜∞

なる｛ξ_k｝によって分割して，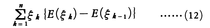

と考えると，（10）の右辺は上の分割を限りなく細かくしていったときの（12）の極限と考えられるから，ふつうの積分の定義と同様に扱って（10）を，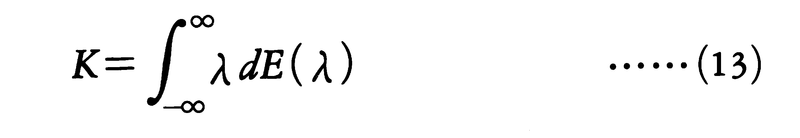

と書く。また，（11）で定義されるE（λ）は射影作用素であって，任意のx∈Xに対して，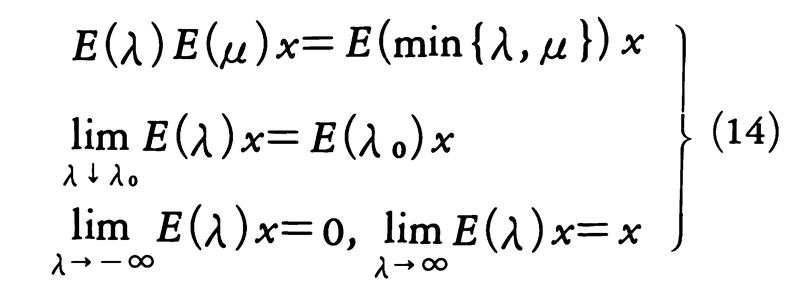

が成り立つ。ヒルベルトによれば，任意の有界対称線形作用素K（完全連続と限らない）に対して，（14）を満たす射影作用素の族｛E（λ）;－∞＜λ＜∞｝が一意的に定まって（13）が成立する。ここでλ₀が固有値であることと，（E（λ）x，x）がλ₀で不連続になるようなxが存在することとは同等である。振動の問題では固有値は振動数に対応するが，光学の言葉に従ってスペクトルとも呼ばれる。一般に，Kが完全連続ならば，（E（λ）x，x）は（10）に現れるλ_iにおいてのみ変化しうるが，どのλ_iをも含まない開区間では変化しない。これに対し，Kが完全連続でないときは，（E（λ）x，x）が連続的に変化しうる区間があることが，ヒルベルトにより発見され，このような区間は連続スペクトルと呼ばれる。このような場合を含み（14）を満たす射影作用素の族｛E（λ）｝を用いて，線形作用素Kを（13）の形に表すことを，Kのスペクトル分解という。

　前に述べた積分作用素がX＝L₂（0，1）全体で定義された有界作用素であるのに対して，微分作用素は一般に，定義域はX全体でないし，有界作用素でもない。有界対称線形作用素の概念を有界とは限らない作用素の場合に拡張したものは自己共役性と呼ばれるが，フォン・ノイマンは前述のスペクトル分解の理論を一般の自己共役な線形作用素の場合に拡張し，それに基づいて量子力学の数学的基礎づけを行った。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」