最大値原理（読み）さいだいちげんり

日本大百科全書(ニッポニカ)

最大値原理
さいだいちげんり

ガウス平面（複素平面）の領域Dで定義された正則関数の絶対値が最大値をとるのは、Dの境界上に限るという定理をいい、応用が広い。同様に最大値原理は、調和関数や、もっと一般に楕円(だえん)形の偏微分方程式の境界値問題の解に対してもいえる。これから、解の一意性が導かれる。

［洲之内治男］

ポントリャーギンの最大値原理

ある種の微分方程式は、それと同等な変分問題（汎(はん)関数の極値問題）に帰着させることができる。制御の問題に対し、ポントリャーギン関数の極値問題にすることを、ポントリャーギンの最大値原理という。

〔例〕実軸上の－1の点に静止している質量1の質点を加速して点1まで運び、そこで速度0になるように、しかも、もっとも速く点1に到達させるには、どのような操縦をすればよいか。ただし、加速度は|u(t)|≦1とする。

　この問題は、関数u(t)（これを制御関数という）を求めることになるが、これを数式化してみよう。時刻tにおける点の位置をx(t)で表し、y₁(t)＝x(t), y₂(t)＝x′(t)と置くと、y₂(t)が速度、y₂′(t)が加速度になる。与えられた条件は、
　|u(t)|≦1,
　y₁′(t)＝y₂(t), y₂′(t)＝u(t),
　y₁(0)＝－1, y₂(0)＝0, y₁(s)＝1, y₂(s)＝0,
このとき、所要時間を最小にするu(t)を求めよ、という問題になる。この最適解の必要条件を与えるため、ポントリャーギン関数
　H(y, u, p,λ₀)＝p₁y₂＋p₂u－λ₀
を考える。y₁(t), y₂(t), u(t)が前の最小値問題の解であるならば、λ₀,α₁,α₂および関数p₁(t), p₂(t)が決まり、u(t)の連続な点tで、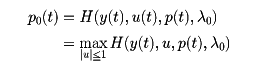

を満足し、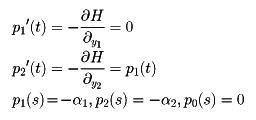

となる、というのがポントリャーギンの最大値原理である。

　ここに得られた関係式から解を求めると、x＝0まではu(t)＝1とし、x＞0ではu(t)＝－1とするのが最適制御で、最小時間は2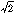となる。

［洲之内治男］

出典　小学館　日本大百科全書(ニッポニカ)