調和関数（読み）ちょうわかんすう（その他表記）harmonic function

改訂新版　世界大百科事典

調和関数 (ちょうわかんすう)
harmonic function

n（≧2）次元ユークリッド空間の領域Dにおいて定義された関数u（P）＝u（x₁，……，x_n）が，連続な2階偏導関数をもち，ラプラスの偏微分方程式，を満たすならば，uはDにおいて調和であるという。

　uがDで調和のとき，任意のP∈Dと，Pを中心とする任意の閉球B⊂D，その表面Sについて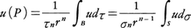，が成り立つ。ここにrはBの半径，τ_nと σ_nはn次元単位球の体積と表面積，dτとdσは体積要素と面積要素を表す。つまりuのPにおける値は，uのBまたはSでの平均値に等しい。これを平均値性質という。逆に，連続性の仮定の下に，この性質をもつ関数は調和関数である（ガウスの定理Gauss' theorem）。

　uがDで調和のとき，uが定数でないかぎり，uはDにおいて最大値も最小値もとらない。したがって，Dがコンパクトであり，しかもuがDの閉包で連続のときは，最大値および最小値はDの境界でとられる。これを最大値の原理という。

　n＝2の場合，調和関数は正則関数と密接な関係がある。まず，正則関数，

　f（z）＝u（x，y）＋iv（x，y）

の実部uと虚部vは，コーシー=リーマンの方程式を満たし，そのことから⊿u＝⊿v＝0が導かれる。すなわちuとvは調和である。逆に任意の調和関数uを領域Dで与えたとき，もしDが単連結ならば，D内の曲線に沿う線積分を用いた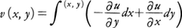，も調和であって，f＝u＋ivは正則関数となる。この事実に基づいて，二次元の調和関数の理論は関数論の重要な1章をなしている。

　ラプラス偏微分方程式に関する境界値問題のうち，次のものをディリクレ問題Dirichlet problemという。領域Dの境界∂Dに関数fを与えたとき，そこでfと一致するようなDの調和関数uを求める。とくに，Dが原点Oを中心とする半径rの球であるとき，∂Dの連続関数fに対するディリクレ問題の解は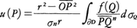，で与えられる。これをポアソン積分Poisson integralという。
執筆者：及川 広太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

調和関数
ちょうわかんすう

n変数の関数u(x₁,x₂,……,x_n)がラプラスの微分方程式

を満足するときこれを調和関数という。ここでは二変数のときに限って述べる。ラプラスの方程式は、電磁気学や流体力学などで、次の形でよく現れる。滑らかな曲線Cで囲まれた領域をDとするとき、C上で与えられた値f(ζ)をとり、D内で調和関数u(x,y)を求めよ、すなわち、
　Δu(x,y)=0　(x,y)∈D
　　u(ζ)=f(ζ)　ζ∈C
を解け、という境界値問題である。とくにCが原点を中心、半径Rの円のときは、解は極座標で表して、ポアソンの積分公式

で表される。調和関数は最大値原理を満たす。すなわち、最大値、最小値をとるのは領域Dの境界上に限る。これから、前の境界値問題の解はただ一つであることがわかる。

［洲之内治男］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

調和関数
ちょうわかんすう
harmonic function

2つの実変数 x ，y の実関数 u(x，y) が，ある領域内で連続かつ1次および2次の偏導関数をもち，2次元のラプラスの方程式 Δu＝∂²u/∂x²＋∂²u/∂y²＝0 を満たすとき，この関数 u(x，y) はその領域において調和であるといい，u(x，y) を調和関数と呼ぶ。調和関数は，n 次元空間内の領域で定義された関数についても，n 次元のラプラスの方程式を満足する関数として，同様に定義する。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の調和関数の言及

【球関数】より

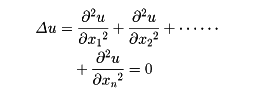
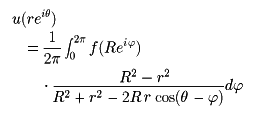
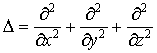…それはもっとも基本的な2階微分作用素であるラプラシアンΔに関係する。3変数x,y,zのときは，であり，Δu(x,y,z)＝0となる関数uを調和関数という。適当な領域で温度分布uを考えたとき，定常状態ならそれは調和関数である。…

※「調和関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」