日本大百科全書(ニッポニカ) 「ラプラス方程式」の意味・わかりやすい解説
ラプラス方程式
らぷらすほうていしき
Laplace's equation
二階線形楕円(だえん)型偏微分方程式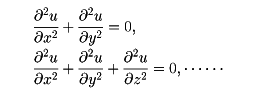
をラプラス方程式といい、均一な等方性媒質の定常状態における温度や静電ポテンシャルなどはこの方程式で表される。
Dを有界な境界Sをもつ平面または空間の領域とする。領域Dでラプラス方程式を満たす2回連続微分可能な関数をD上の調和関数という。
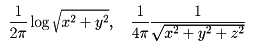
などは、それぞれ平面または空間から原点を除いた領域上での調和関数であり、ラプラス方程式の基本解とよばれる。
D∪S上で連続でS上の各点で与えられた連続関数に等しいD上の調和関数を求める問題を、第1種境界値問題またはディリクレ問題という。Sが滑らかな曲線または曲面のとき、D∪S上で連続でS上の各点でその法線導関数がS上で与えられた連続関数に等しくなるようなD上の調和関数を求める問題を、第2種境界値問題またはノイマン問題という。ノイマン問題の解が存在するためには、与えられた連続関数のS上の積分が0になることが必要であるので、このことが仮定される。それぞれDが有界領域のとき内部問題、非有界領域のとき外部問題とよばれる。
外部問題の解に対しては、二次元の場合、x2+y2→∞のとき有界、三次元の場合、x2+y2+z2→∞のとき0に収束するという条件を課す。これらの条件の下で、ディリクレ問題の解は一意的であり、ノイマン問題の解は定数項を無視すれば一意的である。いずれの問題も、境界SがC2級ならば解が存在する。ただしこの条件は、とくにディリクレ問題についてはもっと弱めることができる。調和関数の性質から、これらの解は領域Dで実解析的である。
Dを平面の領域とする。g(x,y;x0,y0)が(x0,y0)∈Dを固定するとき(x,y)の関数としてD上の調和関数で、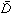 上で連続、S上で0であるとき
上で連続、S上で0であるとき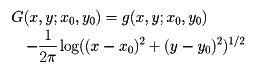
を領域D上のグリーン関数という。Sが十分滑らかならば、Dに対するグリーン関数が存在して、内部ディリクレ問題の解は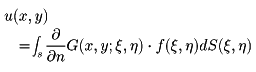
で与えられる。ここでf(ξ,η)はS上で与えられた境界値であり、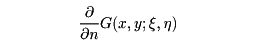
はG(x,y;ξ,η)の(ξ,η)に関する外法線導関数である。ノイマン問題に対するグリーン関数(ノイマン関数)も定義され、同様の積分表示が成り立つ。三次元以上の場合についても同様である。
[小林良和]


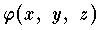 が満足する二階偏微分方程式
が満足する二階偏微分方程式 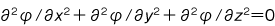 をラプラス方程式という。また,
をラプラス方程式という。また,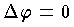 を満足する関数を一般に調和関数という。たとえば,
を満足する関数を一般に調和関数という。たとえば,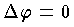 において,
において,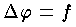 になると,これは
になると,これは