極と極線（読み）きょくときょくせん

日本大百科全書(ニッポニカ)

極と極線
きょくときょくせん

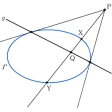
二次曲線Γと点Pが与えられたとする。Pを通る直線とΓとの交点をX、Yとするとき、X、Yに関するPの共役点（すなわちP、Q、X、Yが調和列点となるときの点Q）は直線をPの周りに動かせば一つの直線g上にある。gをPの極線、これに対してPをgの極という。極と極線に関するもっとも基本的な定理は次である。

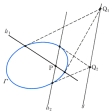
　「Γに関して点Pの極線gが点P′を通れば、P′の極線g′はPを通る」。このとき点PとP′（および直線gとg′）はΓに関して互いに共役という。Γが円錐(えんすい)曲線（楕円(だえん)、双曲線、放物線）の場合、点PがΓ上にあれば、gはPにおけるΓの接線である。PがΓの外にあれば、PからΓに2本の接線を引いて図Aのようにgをつくればよい。PがΓの内部にあるときは図Bによる。すなわち、Pを通り任意に直線h₁、h₂を引き、図BのようにしてQ₁、Q₂を求める。h₁はQ₁の、h₂はQ₂の極線になるから、定理によってPの極線gは2点Q₁、Q₂を通る直線である。極と極線の関係は射影変換で不変な性質であって、射影幾何学において華麗な多くの定理を生み出している。

［立花俊一］

[参照項目] | 調和列点

極と極線（極が二次曲線の外にある場合）…

極と極線（極が二次曲線の内部にある場合…

出典　小学館　日本大百科全書(ニッポニカ)