置換群（読み）ちかんぐん（その他表記）permutation group

改訂新版　世界大百科事典

置換群 (ちかんぐん)
permutation group

集合MからM全体への1対1の写像をMの置換という。Mの置換全体をS（M）で表すと，写像の合成を乗法としてS（M）は群になる。この群S（M）をMの上の対称群という。S（M）の単位元は恒等写像であり，f∈S（M）の逆元は逆写像f⁻¹である。S（M）の部分群はMの上の置換群と呼ばれる。Mの元数がnのとき，S（M）はn次対称群と呼ばれる。M＝｛1，2，……，n｝のときと同型であるので，以下，M＝｛1，2，……，n｝とし，S（M）をS_nで表す。S_nの元σについて，σ（i）＝a_iのとき，σを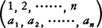で表す。

σ（a₁）＝a₂，σ（a₂）＝a₃，……，σ（a_r-1）＝a_r，σ（a_r）＝a₁で，σがa₁，……，a_r以外の元を動かさない（自身に写す）とき，σは巡回置換であるといい，σ＝（a₁，……，a_r）と表す。r＝2のときが互換である。S_nの中で偶置換全体A_nは正規部分群になる。この置換群をn次の交代群という。n≧5ならば，A_nは自分自身と単位元のみからなる部分群以外には正規部分群をもたない。このことは方程式の可解性と深い関係がある。
→ガロアの理論
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

置換群
ちかんぐん
permutation group

n 個のものの置換
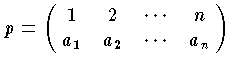の全体から成る集合 P＝{p} は，乗法を結合法として1つの群をつくる。この P を置換群という。もちろん P においては，結合法則が満たされている。しかし，n≧3 なら可換ではない。

出典　ブリタニカ国際大百科事典 小項目事典