改訂新版 世界大百科事典 「ガロアの理論」の意味・わかりやすい解説
ガロアの理論 (ガロアのりろん)
Galois theory
ガロア理論ともいう。高次方程式の解法に関する研究に伴って，18世紀後半に根の性質の解明が進み，1820年代に入ってから，É.ガロアが〈方程式の根をつけ加えた体〉および今日の言葉で〈方程式のガロア群〉と呼ばれるものを考え，部分群と部分体との対応を示した。その結果は，19世紀末ごろJ.W.デデキント，1910年シュタイニッツErnst Steinitz（1871-1928）によって有限次代数拡大体の場合に一般化され，また，28年にはクルルWolfgang Krull（1899-1976）が位相群の概念を利用して，無限次代数拡大の場合に一般化した。
これらの結果の応用，あるいは環のガロア理論への一般化などがあるが，最も基本的な数体の場合を中心にして説明する。
定義
複素数からなるある体（有理数全体を含み，その元の間で四則演算が0で割ることを除いて可能な集合）K，Lについて，LがKのガロア拡大体（または，正規拡大体）であるとは，次の（1）～（3）が満たされるときにいう。
（1）LはKの拡大体。（2）Lの各元αはK上代数的，すなわち，適当な自然数nおよびKの元c1，c2，……，cnをとれば，αn＋c1αn⁻1＋c2αn⁻2＋……＋cn＝0である。（3）各α∈Lに対して，そのK上の最小多項式f（x）（（2）におけるn，ciによる多項式xn＋c1xn⁻1＋……＋cnのうち，nの最小のもの）をとれば，f（x）はLの適当な元 α1，α2，……，αnにより，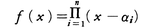
と一次式の積に因数分解される。（3）の条件を確かめるには次の定理が有効である。
定理
（1）f（x）がKに係数をもつn次多項式であるとき，そのn個の根α1，……，αnをKにつけ加えた体（Kの元とα1，……，αnとによって四則演算で得られる数全体の集合）はKのガロア拡大体である。
（2）Kのガロア拡大体L1，L2，……があるとき，それらを含む最小の体もKのガロア拡大体である。
ガロアの基本定理
LがKのn次のガロア拡大体（nはLをK上のベクトル空間と考えたときの次元）であるとき，Lの自己同型σ（LからLへの1対1写像で，σ（a＋b）＝σ（a）＋σ（b），σ（ab）＝σ（a）・σ（b）となるもの）で，そのKへの制限が恒等写像（a∈Kならばσ（a）＝a）であるもの全体Gはn個の元からなる群をなす。このGをこのガロア拡大のガロア群という。このとき，
（1）Gの部分群Hに対し，φ（H）＝｛x∈L｜≏σ∈H，σ（x）＝x｝はKとLとの中間の体になる。逆に，KとLとの中間の体Mをとれば，ψ（M）＝｛σ∈G｜≏x∈M，σ（x）＝x｝はGの部分群になる。この対応φ，ψは互いに逆対応であり，したがって，KとLとの中間体全体とGの部分群全体とがψによって1対1対応する。そしてMがM′の部分体であることとψ（M）がψ（M′）を含むことが同値である。
（2）MがKのガロア拡大であるための必要十分条件は，ψ（M）がGの正規部分群であることである。
一般の体の場合は，正規拡大はまったく同様に定義し，分離的（最小多項式が重根をもたない）という条件を付加してガロア拡大を定義する。ガロア拡大については，上と同じ型の定理が成り立つ。
執筆者：永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報