臨界制動（読み）りんかいせいどう

最新 地学事典

りんかいせいどう
臨界制動

critical damping

固有周期2π/nをもつ振子が流体抵抗2εẋを受けて自由振動をする場合，この振子の変位ẋに関する式はẍ＋2εẋ＋n²x＝0であるが，A₁, A₂をいずれもある初期条件で決まる定数とすれば，この解は次の三つの場合でそれぞれ違った形になる。1）ε＜nの場合，x＝e^－εt（A₁cos 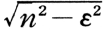t＋A₂sin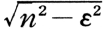t）で減衰振動（damping oscil-lation）をする。xの相次ぐ山，谷の片振幅値は一定の比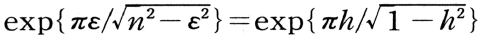，，h＝ε/n（減衰係数）で減っていく。この比をvと書き，減衰比または減衰度（damping ratio）と呼ぶ。vの常用対数値が対数減衰率（logarithmic decrement）。2）ε＞nではx＝A₁e^－α1t＋A₂e^－α2t, α₁＝ε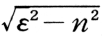＋, α₂＝ε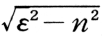－。ε＞nだから，α₁，α₂ともに実数となり，xは振動せずに指数関数的に減るだけ。3）ε＝nのときはx＝（A₁＋A₂t）e^－ntでこれも振動しない。結局1）のε＜nのときだけ振子は減衰振動をする。つまりε＝nは，振子が振動するかしないかの境界条件で，h＝1に相当する。この大きさの減衰を臨界減衰または臨界制振ともいう。h＞1ならば過減衰である。参考文献：萩原尊礼（1957） 振動測定，宝文館

執筆者：三東 哲夫

出典　平凡社「最新 地学事典」

ブリタニカ国際大百科事典 小項目事典

臨界制動
りんかいせいどう

「過減衰」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典