減衰振動（読み）ゲンスイシンドウ

デジタル大辞泉

げんすい‐しんどう【減衰振動】

外力の作用を受けて、時間の経過とともに振幅が減少していく振動。

出典　小学館

精選版 日本国語大辞典

げんすい‐しんどう【減衰振動】

1. 〘 名詞 〙 時間とともに振幅が減っていく振動。空気の抵抗や摩擦などによって、振動のエネルギーが減少していく現象。減幅振動。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

減衰振動
げんすいしんどう

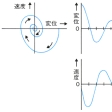
質点が1直線に沿って振動するとき、質点をその直線上の原点に引き戻す復原力のほかに、質点の運動を妨げる抵抗力も働くと、振動の振幅は時間の経過とともに指数関数的に減少する。このような振動を減衰振動という。質点の原点からの変位が小さければ、復原力は変位に比例し、質点の速度が小さければ、抵抗力は質点の速度に比例する。この場合には、質点の運動方程式は2階線形常微分方程式で、その解は容易に求められるので、この場合について減衰振動を論ずることが多い。この場合には、振動の1周期ごとに振幅が減少する割合の自然対数の絶対値が、時間と無関係な一定値となる。この値は対数減衰率とよばれる。抵抗が大きい場合には、振動が1回おこるか、またはまったく振動しないで、質点の原点からの変位が時間とともに指数関数的に減少する。このような運動は過減衰とよばれる。減衰振動と過減衰の中間に、臨界制動とよばれる状態があり、振動の減衰がもっとも短い時間の間におこる。一般に、本来の減衰振動だけでなく、過減衰と臨界制動の運動も、広く減衰振動とよぶことが多い。

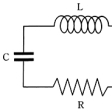
　質点の1直線に沿っての振動に限らず、物体をつるした糸のねじれ振動で空気の抵抗がある場合や、コンデンサーC、コイルLおよび電気抵抗Rを直列につないだ電気回路における電気振動など、各種の振動において、減衰振動が生ずる。減衰振動をする質点の力学的エネルギーは時間の経過とともに失われるが、これは摩擦熱に変化する。回路の電気振動においては、電磁場のエネルギーが時間の経過とともに失われ、ジュール熱に変化する。

［飼沼芳郎］

質点の変位と速度の振幅

コンデンサー、コイル、電気抵抗を直列に…

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

減衰振動
げんすいしんどう
damped oscillation

振幅が時間とともに減少していく振動。振動系に復元力のほかに抵抗や摩擦などの制動力が働くときに起る。制動力が復元力に比べて小さい場合には，空気中の振り子のように何回も振動しながら振幅が次第に小さくなる。この減衰振動は，時間 t とともに振幅 Ae^-βt が指数関数的にゆっくり減少する単振動とみなすことができる。βは減衰定数と呼ばれ，制動力が大きいほど大きくなって，振幅の減少が速くなる。制動力が働かない単振動の周期に比べて，減衰振動の周期は大きくなる。制動力が大きくなると，もはや振動しないで，時間とともにゆっくり平衡点に近づく。これを過減衰という。減衰振動から過減衰に移る境界を臨界減衰という。広い意味ではこれらも減衰振動と呼ばれる。臨界減衰の場合に減衰が最もすみやかなので，計器類の指針，自動シャッタなどでは速く所定の位置で止らせるために，ちょうど臨界減衰となるように調整された抵抗が加えてある。減衰振動では抵抗や摩擦によって振動エネルギーが失われる。電気振動は電気抵抗によるジュール熱の発生や電磁波の放射でエネルギーを失って減衰する。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

減衰振動【げんすいしんどう】

時間がたつにつれて振幅が次第に小さくなる振動。振子や弾性体の振動では摩擦や抵抗のため，電気振動ではジュール熱や電波の放射のため減衰振動となる。自然界の自由振動はすべて減衰振動で，振幅がいつまでもかわらない非減衰振動を起こすには外からエネルギーを供給しなければならない。→減衰定数
→関連項目振動

出典　株式会社平凡社

世界大百科事典（旧版）内の減衰振動の言及

【振動】より

…このとき回路には周期的に変化する振動電流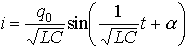，が流れる。
［減衰振動］
　調和振動は，いったん振動を開始すると理論上はそれが永久に続くはずである。しかし実際に振子を振らせると，しだいに振れが小さくなって，やがて静止してしまう。…

※「減衰振動」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」