精選版 日本国語大辞典 「指数」の意味・読み・例文・類語
し‐すう【指数】
- 〘 名詞 〙
- ① 数学で、累乗を表わすために、数字または文字の右肩につける小さな数字または文字。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
- ② ある抽象的な事柄の程度を、数の大小によって示すために、何らかの方式により表わした数値。
- [初出の実例]「ホイ駕籠が馬車に変じ、猪牙船が小蒸汽に変じ、其他斯くの如きもの指数に勝へざるが如くにして」(出典:一年有半(1901)〈中江兆民〉附録)
- ③ 物価や賃金などの年ごと、または月ごとの変動の模様をわかりやすく示すために、ある年またはある月のそれを一〇〇として表わした数字。
- [初出の実例]「本年一月の平均指数一三〇なりしもの、十一月に至りて一二二に落ち」(出典:東京朝日新聞‐明治四一年(1908)一二月三一日)
改訂新版 世界大百科事典 「指数」の意味・わかりやすい解説
指数 (しすう)
(1)数学の分野で種々の異なった意味で用いられる。正数aをとり,そのx乗axを考えるとき,xのことをべき指数power exponent,または単に指数exponentと呼ぶ。代数学の分野では,例えば群Gの部分群Hがあるとき,その左または右剰余類の個数をHの指数indexという。また積分作用素の同一固有値に対応する一次独立な固有関数も指数と呼ばれる。多様体には位相不変量としての指数がある。
執筆者:飛田 武幸(2)統計用語としては,ある状態から他の状態へ移ったときの数量の相対的増減を測定するための指標を指数indexあるいはindex numberといい,通常それはある一つの選ばれた状態の数量に対するそれと比較されるべき状態の数量の比率に100を乗じたものとして定義される。比較される二つの状態には何の制約もなく,二つの異なる時点(例えば二つの年)でも,二つの異なる場所(例えば二つの都市)でも,また二つの異なる個人のグループ(例えば年金受給家計のうちの単身世帯と2人世帯)でもよい。
指数はその定義より,ある一つの選ばれた状態が100として表現されることがわかる。これは指数系列の参照基準,あるいは比較基準と呼ばれている。年次系列を例にとってみると,100の水準として定めた年(これをとくに基準年次という)が参照基準であり,これと比較される年(これをとくに比較年次という)は例えば指数150というようになる。これは比較年次の大きさは基準年次の水準の1.5倍であることを意味している。
指数が効果をあらわすのは,いくつかの数値の系列を総合して一つの系列にまとめ上げる場合である(ただ一つの数値の系列を指数化することは簡単であり,そうすることは有効数字の多い統計をわかりやすく表現したりする場合にしか意味をもたないであろう)。例えば,消費者物価指数のように,消費者が購入する多数の財・サービスの小売価格から一つの集計された指数をつくる場合がそうである。このときには,計測された価格データをそのまま平均するわけにはいかないから,まず各価格をそれぞれの基準年次の価格に対する比率に直し,その後にそれらを何らかの形で平均するという方法が用いられる。この平均にあたって実際によく用いられるのは,基準年次における支出構成比をウェイトとした加重算術平均算式である。これをラスパイレス算式(〈ラスパイレス指数〉の項目参照)という。これ以外のものとしては,比較年次における支出構成比をウェイトとして用いるパーシェ算式(〈パーシェ指数〉の項目参照),ラスパイレス算式による指数とパーシェ算式による指数の幾何平均をとるフィッシャー算式(〈フィッシャーの理想算式〉の項目参照)などがあげられる。
経済量に関係する指数に限っていえば,これは物価指数と数量指数の二つに分けられる。経済量は金額で表現されるものが多いが,金額で表された経済量の系列は価格の変化と数量の変化に分解される。物価指数はこれらのうちの価格の変化部分を,数量指数は数量の変化部分を表すために作成される指標といえる。物価指数の例としては,先にあげた消費者物価指数,卸売物価指数,小売物価指数,生計費指数および株価指数などがあげられる。また,数量指数の例としては,鉱工業生産指数,農林水産生産指数,雇用指数,出荷指数などがあげられる。数量指数の場合にも物価指数の場合と同じように先に述べた指数計算上の総合の問題があるが,なかには雇用指数のようにそうした問題がないものもいくつか含まれている。
執筆者:貝山 道博
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「指数」の意味・わかりやすい解説
指数
しすう
index number
ある特定データ系列の変動の把握、同種の複数データ系列間の変化の比較、あるいは多数の要素から構成される一群の対象の動きを総合的に理解することなどを目的に、ある基準値と容易に比較可能なように作成された統計値のこと。どの指数にも基準値のあることは共通であるが、その対象と目的に応じて指数の作成方式には種々のものがある。ある特定データ系列の変動や同種の複数データ系列間の動きをみるためには、個々のデータ系列について、特定観測値(時系列データの場合には特定時点のデータ、横断面データの場合には特定内容のデータ)を基準値として、通常100と置き換え、それに従って他の観測値を比例計算で算定し直すことにより、指数系列を作成する。このようにして作成されたものは単純指数とよばれ、個々の製品の生産動向の調査や国民所得の伸びの国際比較など、広い範囲にわたって作成、利用される。これに対して、多数の要素から構成される対象の動きを全体的に把握するために、個々の要素の観測データを総合して作成される指数は、総合指数とよばれる。これには景気動向指数のように個々の単純指数の変動方向を単に割合として作成されるものもあるが、一般には、個々の構成要素が対象全体のなかに占める重要性を考慮するためのウェイト(加重)を用いて算定される。そのもっとも代表的なものとしては、物価指数、生産指数、貿易指数などがある。その算式も、ウェイトの採用の仕方によって、ラスパイレス算式、パーシェ算式、エッジワース算式の相違があり、さらに前の二算式を混合して作成するものとしてフィッシャーの算式がある。
[高島 忠]
普及版 字通 「指数」の読み・字形・画数・意味
【指数】しすう
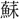 轍〔黄州快哉亭記〕蓋(けだ)し亭の見る
轍〔黄州快哉亭記〕蓋(けだ)し亭の見る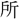 、南北百里、東西一舍。~西のかた武昌の
、南北百里、東西一舍。~西のかた武昌の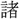 山を
山を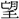 めば、岡陵
めば、岡陵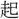 伏し、
伏し、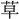 木行列し、畑
木行列し、畑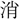 え日出で、漁夫樵
え日出で、漁夫樵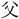 の舍、皆指さし數ふべし。此れ其の快哉(くわいさい)と爲す
の舍、皆指さし數ふべし。此れ其の快哉(くわいさい)と爲す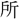 以の
以の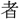 なり。
なり。字通「指」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
百科事典マイペディア 「指数」の意味・わかりやすい解説
指数【しすう】
→関連項目常用対数|べき(冪/羃)
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「指数」の意味・わかりやすい解説
指数
しすう
index
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の指数の言及
【群】より
… 方程式が代数的に解けるための条件は,ガロア群がこの性質をもつことであるという理由で,このように名づけられたのである。
[指数と位数]
Hが群Gの部分群であるとき,互いに異なる右剰余類Haの数(無限の場合も考える)をHのGにおける指数という。[G:H],(G/H)などで表される。…
【整数論】より
… rがpの一つの原始根であれば,1,r,r2,……,rp-2は,どの二つも互いに合同でなく,これらが既約剰余類の代表系を与え,したがってpと互いに素な整数aに対して, a≡rα (mod p) (0≦α<p-1) を満たす整数αがただ一つだけ定まる。このことをrを底とするaの指数といい,Indr(a)で表す。p=11のとき,rとして2をとると,Indr(a)は次の表のようになる。…
【統計】より
…
[加工統計]
統計調査の結果から,いろいろな加工データが作られる。その一つは指数であり,生産指数,物価指数などが計算されている。また多くの経済データを統合して国民経済全体の動きをまとめたものに国民経済計算体系があり,経済企画庁で毎年計算,公表している(〈国民経済計算〉の項参照)。…
【モース理論】より
…ふつうにはこのとき,標高aの等高線f-1(a)と標高bのそれf-1(b)とは,aとbとの間にfの極値,すなわち山頂,谷,鞍点がまったく現れなければ,位相的には同じ形をしており,また逆に,極値が現れて,形が崩れる場合は,崩れ方が極値の状態(それが山であったか谷か鞍か)によって支配されていることもわかる。この事実を一般の微分可能多様体Xと,その上の微分可能な関数fに対して拡張したものがモースの指数定理であり,モースの理論の骨子をなすものである。すなわち,非退化なfの極値を,0からXの次元までの整数(これを指数という)によって分類し,各指数の極値が現れるときの等高線f-1(a)の形の崩れ方を,位相幾何学的な方法によって表現したものが,指数定理にほかならない。…
※「指数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

