連分数（読み）れんぶんすう

日本大百科全書(ニッポニカ)

連分数
れんぶんすう

分数のうち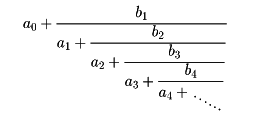

という形式を連分数という。これを簡単に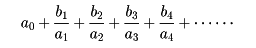

と表す。有限で切れる連分数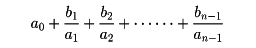

は単に分数P_n/Q_nに直せる。その列が一つの数ωに収束するとき、連分数は収束するといい、ωを連分数の値と称する。たとえば

である。とくにa₀が整数、b_nが1、a_nが自然数の場合を正則連分数という。前式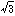の展開が正則連分数である。任意の無理数はただ一通りに正則連分数に展開され、逆に正則連分数はつねに収束して無理数を表す。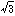の場合、分母に1と2が交互に表れるが、このように、あるところから先が循環する正則連分数を循環連分数という。無理数ωを表す正則連分数が循環連分数であるための必要十分条件は、ωが整数係数の二次方程式の解となることである。

　正則連分数の近似分数P_n/Q_nは
　　P_n+1=P_na_n+P_n-1,
　　Q_n+1=Q_na_n+Q_n-1
　　　　　(n≧1,P₀=1,Q₀=0)
という漸化式によって定まる。したがって
　　P_nQ_n-1-P_n-1Q_n=(-1)ⁿ
なる関係が成り立つ。これらの性質を用いて、連分数は不定方程式、ディオファントス近似、代数方程式の根(こん)の近似値などに有効に用いられる。たとえばa、bを整数として
　　ax-by=1, (a,b)=1
なる一次不定方程式を考える。a/bを正則有限連分数に展開して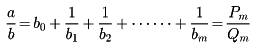

とすると、
　　x₀=(-1)^m-1Q_m-1,
　　y₀=(-1)^m-1P_m-1
によって一つの解が与えられる。他の解はすべて
　　x₀+bt,　y₀+at　（tは整数）
と表せる。

［足立恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

連分数 (れんぶんすう)
continued fraction

a₀，a₁，……，a_nおよびb₁，b₂，……，b_nの式，

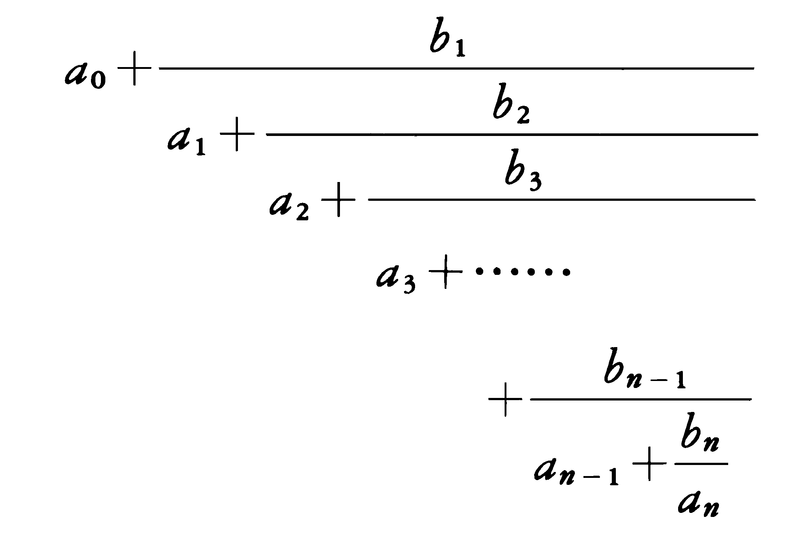
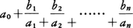を連分数という。この連分数を表すのに記号，を用いる。上のように有限で終わるものを有限連分数といい，無限に続くものを無限連分数という。b₁＝1，b₂＝1，……，b_n＝1となるものを正則連分数といい，以下ではこの場合について述べる。実数xに対して，［x］（［　］はガウス記号）で，xをこえない最大の整数を表すことにする。実数ωに対して，k₀＝［ω］とおけば，と表せる。次にω₁が整数でなければ，k₁＝［ω₁］とおいて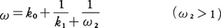，と表せる。同様の計算を続けると，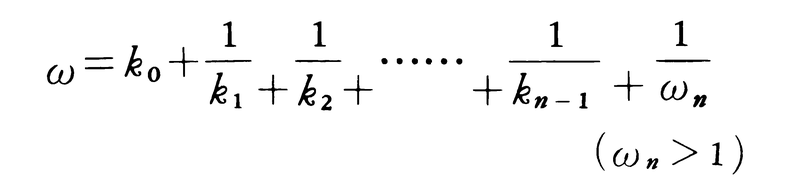

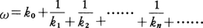となる。ωが有理数であるときには，ω_nはあるところで整数となり，したがってωは有限連分数で表せる。逆に有限連分数は有理数である。次にωが無理数とすると，ω_nは整数とはならず，ωの無限連分数展開，を得る。数列k₀，k₁，……，k_n，……の中に，あるところから先は同じ数字の配列が繰り返し現れるものを循環連分数というが，このような連分数は，有理数係数の二次方程式の根となっているような無理数，すなわち二次無理数を表している。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

連分数
れんぶんすう
continued fraction

図のような形の分数をいう。これを簡単に表わすと，
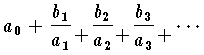となり，無限に続くものを無限連分数という。また，次のように
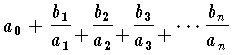と有限で切れるものを有限連分数という。

出典　ブリタニカ国際大百科事典 小項目事典