分数（読み）ブンスウ（その他表記）fraction

デジタル大辞泉

ぶん‐すう【分数】

二つの整数a・bの比として表される数。零ではない整数aで整数bを割った結果をb/aと表したもの。あるいは、1をa等分したものをb個集めた大きさをb/aと表したもの。横線の下を分母、上を分子とよぶ。

出典　小学館

精選版 日本国語大辞典

ぶん‐すう【分数】

1. 〘 名詞 〙
2. ① 身についた天の理数。
   1. [初出の実例]「分数之理可_レ悲」(出典：玉葉和歌集‐承安元年（1171）七月一〇日)
   2. [その他の文献]〔淮南子‐主術訓〕
3. ② 暦数の区分。〔漢書‐律暦志上〕
4. ③ 整数ａを零でない整数ｂで割った商を、横線を用いてa/bと表わしたもの。ａを分子、ｂを分母と呼ぶ。有理数。
   1. [初出の実例]「fraction （分数）」(出典：百学連環（1870‐71頃）〈西周〉一)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

分数
ぶんすう
fraction

自然数m、nについて、1をm等分したものをn個集めた大きさを、横線を用い、その下にm、その上にnを書いて、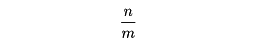

のように表す。これが分数である。分数n/mで、mを分母、nを分子という。また分数n/mは、分子nを分母mで割った商とみられる。つまりn÷m=n/mである。

　分子が1である分数を単位分数という。n/mは、単位分数1/mのn個の和といえる。分子と分母の等しい分数m/mは1に等しい。分子が分母より小さい分数は1より小さく、真分数(しんぶんすう)といい、分子が分母より大きい分数は1より大きく、仮分数(かぶんすう)という。つまり分数n/mは、nがmより小さいとき真分数、nがmより大きいとき仮分数である。分数と整数の和、たとえば2/3と4の和を、＋記号を省略し、整数と分数を並べて、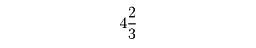

のように表す。これも分数に入れて、帯分数(たいぶんすう)という。1より大きい仮分数は帯分数に表すことができる。また逆に、帯分数は、たとえば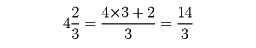

のように仮分数に表すことができる。

　自然数自身、分数の特別なものとみることができる（例　2=6/3）。

　分数には、表し方が違うが、同じ大きさのものがある（例　2/3=4/6=6/9=8/12）。ある分数の分子、分母に同じ整数を掛けると等しい分数が得られる。また分子、分母が公約数をもつとき、それで分子、分母を割ると等しい分数が得られる。これを約分という。

　例　10/15=(5×2)/(5×3)=2/3
　二つの分数n/mとs/rが等しいのは、n×r=m×sのときである。分母の違う分数がいくつかあるとき、分母が同じで、それぞれ等しい分数に表すことができる。これを通分という。

　例　(2/3,5/8)=(16/24,15/24)
　分母が同じ分数は、分子が大きいほうが大きい。分母が違う分数では、通分して分母を同じに表してから比べればよい。

　分数の四則計算は、次のようになされる。

　分母の同じ二つの分数の和・差は、その分母を分母とし、分子の和・差を分子とする分数である。

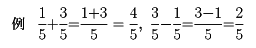
　分母が違う分数の和・差は、通分して分母が同じ分数に表し、前記の方法で計算する。

　二つの分数の積は、それぞれの分母の積を分母とし、分子の積を分子とする分数である。

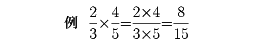
　分数の商は、割られるほうの分母と割るほうの分子の積を分母とし、割られるほうの分子と割るほうの分母の積を分子とする分数である。

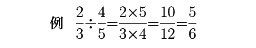
　分数n/mに対し、その分母と分子を入れ替えた分数m/nを、元の分数の逆数という。分数の商は、割られる分数と、割る分数の逆数の積として求められる。帯分数の積・商は、それぞれを仮分数に表してから、前記の方法で計算する。

　分数は、自然数の商からさらに拡張して考えられる。整数nを0でない整数mで割った商を考え、n/mと表す。このとき、計算についての規約から、分母のmの符号はいつでも正とすることができる。そして、分子nが正のときが正の分数、負のときが負の分数である。

　分数の分母や分子が分数であることもある。これを繁分数(はんぶんすう)という。

　例　(2/3)/(4/5)、これは2/3÷4/5のことである。

　さらに分母や分子が無理数のこともある。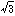/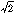などがそれで、このとき、それと同じ大きさで、分母を有理数のものに表すことができる。これを分母の有理化という。分母の有理化の際は、分子、分母に同じ数を掛けても分数の大きさが同じであることを使う。

　例1　3/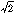では、分母の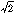について、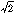（）²=2であることから、分子と分母に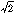を掛ける。

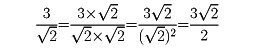
　例2　2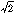/(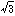+1)では、(a+b)(a-b)=a²-b²の公式を利用し、分子と分母に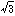（-1）を掛ける。

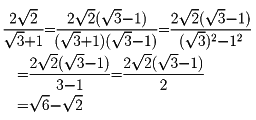
［三輪辰郎］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

分数 (ぶんすう)
fraction

\(\frac{1}{2}\)，\(\frac{2}{3}\)のように，二つの数の比の値を表すのに，横線の上下に数を配置して表したものを分数という。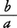と書いた場合b÷aの値を表し，aを分母と呼び，bを分子と呼ぶ。印刷などのつごうでb/aの形に，斜めの線を使うこともある。数としては1/2＝0.5であるが，0.5は小数であって分数ではない。分数は数を表すと同時に，表し方も含めた言い方なのである。通常，分数というときは，分母，分子ともに整数（分母は0でない）のときに限るが，そのように限定しないで分数ということもある。しかし，そのような場合は〈分数形〉と呼ぶことがふつうである。その一例は分母，分子の一方，または両方が分数である場合で，これはとくに繁分数と呼ばれる。

　一つの分数b/aの分母，分子に0でない数cを掛けたbc/ac，cで割った（b/c）/（a/c）を作っても分数の値は変わらない。分母，分子が自然数の分数b/aにおいて，b≧aのときb/aは仮分数であるといい，b＜aのときb/aは真分数であるという。b/aが仮分数であるとき，その値は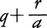（q，rはそれぞれbをaで割ったときの商と余り）である。この値を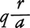と表すことができ，この形に表したとき帯分数という。qと\(\frac{r}{a}\)（またはqか\(\frac{r}{a}\)）と読む。帯分数は分数の値の大きさがある程度わかりやすいという理由で，小学校教育において利用されるが，乗法，除法の際には不便であるので，中学以後ではあまり用いられない。

　分数の乗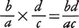法は，除法は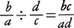，でわかりやすいが，加法と減法は複雑である。根本原理は〈分母が同じ分数の加・減は，分母は同じで分子の加・減を行う〉である。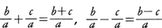したがって，加法，減法は通分をしてから行うのである。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

分数
ぶんすう
fraction

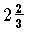分数の使用は古代文化からみられるが，それは各文化によって差異があり，また近代の使用とも異なる。エジプトで用いられたのは主として単位分数だけであり，ギリシアのピタゴラス派は2つの量 A と B を共通単位 M をもってきて，A＝aM，B＝bM と整数 a と b で表わすときの比の a：b として分数を考えた。これは除法と結びついて，近代ヨーロッパの a÷b＝a/b へとつながっていく。中国では三分之二というように，3分した単位による2という発想が強く，日本語の表現からして，「3つに分けた2つぶん」というこの発想を強く受けている。近代的には，実数概念が確立されて以後，普遍的な量としての数直線に埋込まれた形で考えられるようになった。分数の表現には， すなわち 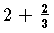といった整数部分を取出した帯分数による表現と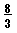， のように分子に整数部分も組入れた仮分数による表現とがある。小学校では前者を多用し，中学校以後は後者をよく用いるようになる。これは，帯分数のほうが量を表わして加法と結びつきやすく，仮分数のほうが乗法と関係させて使いやすく，しかも分数が乗法と関係して使われる場面が多くなり，また文字式を使用するときの乗法記号 × の省略と混乱しやすいなどの理由による。 2/3 のように分子が分母より小さい場合は，帯分数の特別の場合とも仮分数の特別の場合とも考えられるが，真分数といわれている。全体を3つに分けた2つ，といった歴史的な使用と直接的に結びつくからであろう。 6/9＝2/3 のように，約分によって簡単な表現にすることができて，普通はこれ以上約分できないまで，最も簡単化された表現を使う。これを既約分数という。ただし問題によっては，たとえば 1/6 と 2/6 と 3/6 に分割されるというほうが，1/6 と 1/3 と 1/2 に分割されているというより，事態がはっきりすることもあり，このような場合には，あえて既約でない形で使う。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

分数【ぶんすう】

整数aを０でない整数bで割った商a/bのこと。aを分子，bを分母という。a＜bの場合を真分数，a＞bの場合を仮分数という。仮分数は整数部分と真分数部分に分けることができ，これを帯分数という。分子・分母が公約数をもたないものが既約分数。分数は内容的には有理数と同じだが，一つの有理数はたとえば2/3＝4/6＝6/9＝…のように無数の分数の表示をもつ。

出典　株式会社平凡社

世界大百科事典（旧版）内の分数の言及

【数】より

…
［数概念の発達］
　数概念の出発は，個数を数えることから自然数の概念に到達することであり，いろいろな古代文明において，その段階には到達していた。次の段階は正の分数であるが，この発展については地域による差が大きかった。中国ではずいぶん古くから自然数の十進法による表記法が整い，掛算の九九も整っていて，分数も〈何分之何〉という言い方で，われわれと同様な理解をしていた(九九という語は，古代中国の九九の表が〈九九八十一〉から始まっていたことによる)。…

※「分数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」