不定方程式（読み）フテイホウテイシキ（その他表記）indeterminate equation

デジタル大辞泉

ふてい‐ほうていしき〔‐ハウテイシキ〕【不定方程式】

解が無数にある方程式。そのうち特に、整数を係数として整数解を求める場合の代数方程式をいう。

出典　小学館

精選版 日本国語大辞典

ふてい‐ほうていしき‥ハウテイシキ【不定方程式】

1. 〘 名詞 〙 係数が有理数で、二つ以上の未知数をもつ代数方程式の、特に整数の解を問題にするときの称。ディオファントスの方程式とも。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

不定方程式 (ふていほうていしき)
indeterminate equation

ディオファントス方程式Diophantine equationともいう。方程式3X＋5Y＝1やX²＋Y²＝Z²のような，整数係数の代数方程式の整数解を求めることを不定方程式を解くという。整数解が無限に存在して定まらないことがあるので，不定ということばが用いられている。今日では，方程式の係数や解に関して整数であるという条件のほかに，有理数である，またはある代数体の整数環に含まれるなどの条件を考えることもある。

　不定方程式の歴史は古く，アルキメデスがアレクサンドリアの数学者に提出したと伝えられている〈牛の問題〉は，二次の不定方程式の問題として表される。また3世紀ころ活躍したアレクサンドリアの数学者ディオファントスは多くの不定方程式に関連する問題を考えた。インドにおいても，7世紀ころ，ブラフマグプタは，初めて二元一次不定方程式，

　aX＋bY＝c　　　 （a，b，cは整数）

の一般的な解法を与え，12世紀ころには，バースカラは，後述のペル方程式と呼ばれる二元二次不定方程式の解を求める方法を得ている。17世紀ころ，P.deフェルマーは，ディオファントスの著作に興味をもち，不定方程式を中心に整数論の研究をした。その後も，L.オイラー，J.L.ラグランジュ，C.F.ガウスなど多くの人々により研究が続けられている。1900年のパリ国際数学者会議でD.ヒルベルトが提出した23の問題の第10番目の問題〈不定方程式の整数解が存在するかどうかを，有限回の手段で判定する一般的方法を与える〉は否定的に解決された。

　以下，不定方程式の具体的な例について述べる。

　aX＋bY＝c　

　　（a，b，cは整数）……（1）　

この方程式は，cがa，bの最大公約数で割りきれるときにのみ整数解をもつ。解法を具体例で示す。方程式，

　9X＋29Y＝6　　……（Ⅰ）　　　　

を考える。29を9で割ると，

　29＝3×9＋2

そこで，X′＝X＋3Yと置くと，

　9X′＋2Y＝6

同様にして，9＝4×2＋1からY′＝Y＋4X′と置いて，

　X′＋2Y′＝6

これより，X′＝6－2Y′，したがって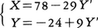，のY′に整数を代入して，（Ⅰ）のすべての整数解を得る。

　a₁X₁＋a₂X₂＋……＋a_nX_n＝b

　　（a₁，……，a_n，bは整数）　　　……（2）　

a₁，……，a_nの最大公約数がbを割りきるときにのみ整数解をもち，（1）と同様の方法で解ける。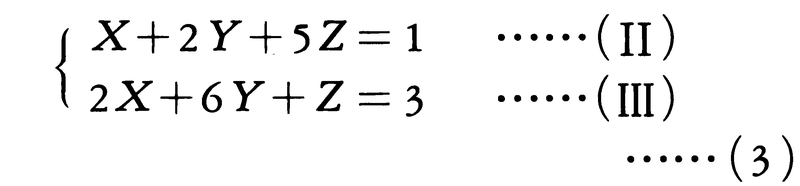

（II）を解いて，

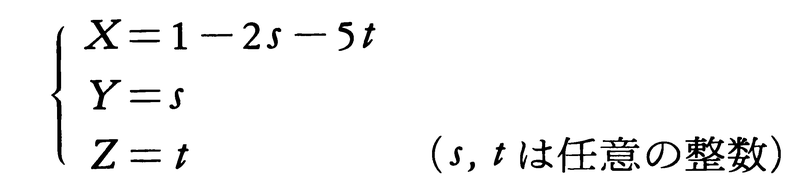
を得る。これを（Ⅲ）に代入して，

　－2s＋9t＝－1

を得る。これからs＝5－9u，t＝1＋2u，したがって（3）の解は，次のように与えられる。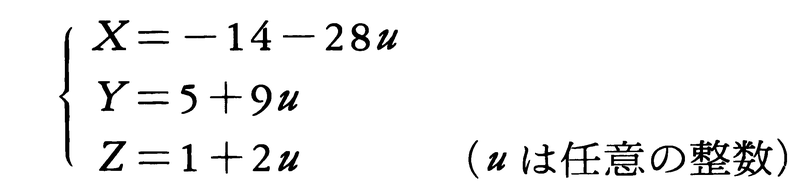

　X²＋Y²＝Z²　　　……（4）　

この方程式の整数解で正のものをピタゴラス数というが，そのなかで，XとYが互いに素なものは，X，Yの一方が偶数になり，それをXとすれば，X＝2mn，Y＝m²－n²，Z＝m²＋n²で与えられる。m，nは，互いに素で，m＞n，かつm＋nは奇数となる正の整数である。

　X²－DY²＝±4 （Dは整数）　……（5）

この方程式は，ペル方程式Pell's equationと呼ばれている。以下Dは，m²（mは整数）の形でないとする。D＜0のときには，整数解は有限個しかないが，D＞0のときには，X²－DY²＝4にはつねに無限個の整数解が存在し，

を最小にするものを，X＝x₀，Y＝y₀とすれば，他のX，Y＞0なる解は，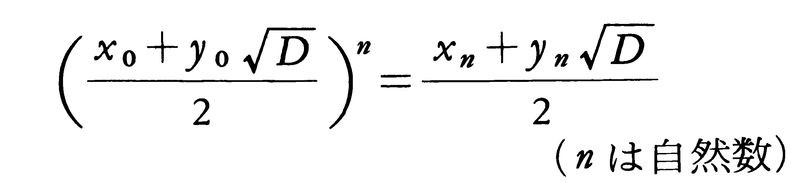

としたとき，X＝x_n，Y＝y_nで与えられる。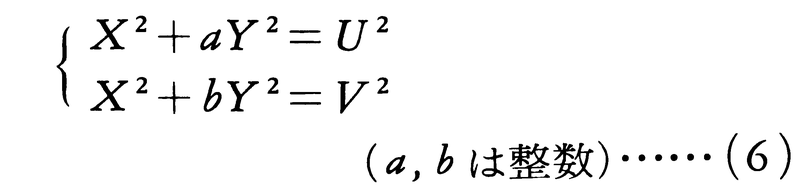

L.フィボナッチとフェルマーによって，a＝1，b＝－1のときには，X＝Y＝U＝V＝0以外に整数解をもたないことが知られている。a＝2，b＝6のときには，L.オイラーが，X＝191，Y＝60，U＝209，V＝241という解を見いだしている。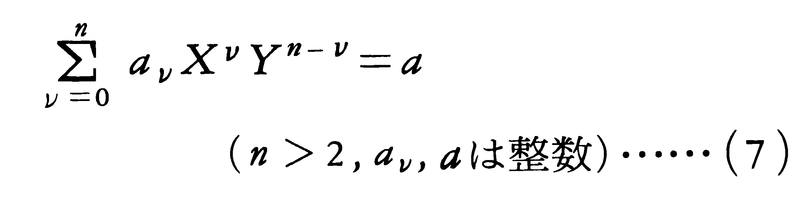

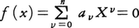が相異なる根をもつとき，（7）はたかだか有限個しか解をもたない（トゥエThueの定理）ことが知られている。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

不定方程式
ふていほうていしき

整係数の代数方程式の整数解、ときには有理数解を求めることを、不定方程式またはディオファントス方程式を解くという。ここに名を残しているディオファントスは3世紀ごろのギリシアの代数学者である。彼の著書『算数論』には不定方程式の研究は含まれているが、すべて有理数解を扱っているのが一つの特徴である。

　たとえば
　　ax+by=c （a,b,cは整数）(1)
　　xⁿ+yⁿ=zⁿ（nは2以上の自然数）(2)
は代表的な不定方程式である。(1)は、aとbの最大公約数がcを割り切るとき解をもつが、その解法としてユークリッドのアルゴリズムが有名である。(2)はn=2のときがピタゴラス数になり、紀元前2000年ころすでに古代バビロニアで研究されたものである。

　近代整数論の始祖とされるのはフェルマーであるが、フェルマーは、ディオファントスの『算数論』中のピタゴラス数に関する記述から、(2)がn≧3のとき自然数解をもたないことに気づいたといわれている。

　近年、ベーカーAlan Baker（1939―　）によって不定方程式に一つの変革がもたらされた。たとえばf(x,y)を既約な三次以上の同次多項式とし、mを0でない整数とすると、不定方程式
　　f(x,y)=m
は有限個の解しかもたない、というのが有名なトゥエA. Thue（1863―1922）の定理であるが、これに対してベーカーは、解の大きさの限界をf(x,y)の係数から与えることに成功したのである。

［足立恒雄］

[参照項目] | フェルマーの予想 | ユークリッドの互除法

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

不定方程式【ふていほうていしき】

一般には，方程式の数が未知数の数より少なく，従って無数の解をもつ方程式。たとえばx−２y＝１。ふつうはさらにいくつかの条件をつけ解を求める。特に整係数の代数方程式の整数解を求める問題が古来興味をもたれ，そのような方程式をディオファントス方程式といい（ディオファントス），単に不定方程式といえばこれをさすことが多い。
→関連項目整数論｜方程式

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

不定方程式
ふていほうていしき

「ディオファントスの方程式」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典