連立方程式（読み）レンリツホウテイシキ（その他表記）simultaneous equation

デジタル大辞泉

れんりつ‐ほうていしき〔‐ハウテイシキ〕【連立方程式】

１ 二つ以上の未知数を含む二つ以上の方程式からなり、これらの方程式が未知数の同じ値によって成り立つもの。未知数の最高次数により、連立二次方程式・連立三次方程式のようによぶ。
２ （比喩的に）問題が複雑にからみ合っている物事のたとえ。「財政再建、福祉充実、景気対策の連立方程式を解くための政策を立案する」

出典　小学館

精選版 日本国語大辞典

れんりつ‐ほうていしき‥ハウテイシキ【連立方程式】

1. 〘 名詞 〙 数学で、二種以上の未知数を含む方程式を二個以上組にしたもの。x+2y=11,3x+y=8 の類。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

連立方程式 (れんりつほうていしき)
simultaneous equation

いくつかの方程式の組を連立方程式といい，それらの方程式すべてをみたすものをその連立方程式の解という。zの関数yについての

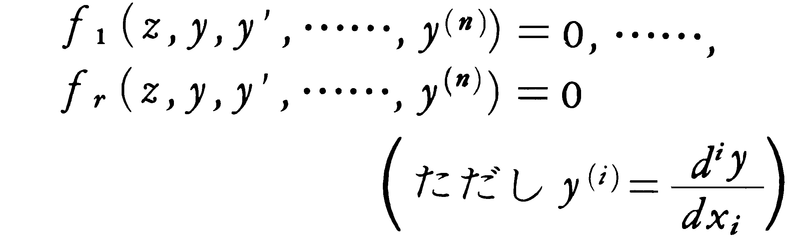
という形の方程式が連立常微分方程式で，これらすべてをみたす関数y（z）がこの連立常微分方程式の解である。yがいくつかの変数の関数であるときには偏微分が現れるが，その場合には連立偏微分方程式という。ある体k上のm変数の多項式f₁（x₁，……，x_m），……，f_r（x₁，……，x_m）を0とおいた連立方程式f₁＝0，……，f_r＝0をm元連立代数方程式という。f₁（a₁，……，a_m）＝0，……，f_r（a₁，……，a_m）＝0となる（a₁，……，a_m）をこの連立方程式の解という。

　以下，連立代数方程式について述べる。連立代数方程式の解全体はm次元空間の中でのf₁（x₁，……，x_m），……，f_r（x₁，……，x_m）の共通零点全体であり，代数多様体をなす。解が一つもないとき，この連立方程式は不能であるといい，解が有限個のとき，正則であるという。解が無限個のとき，不定であるということがあるが，あまりよい言い方ではない。連立代数方程式を解くのには消去法を使えばmが少ない場合に帰着できる。r＝1のときはかってなa₂，……，a_mについてのf₁（x₁，a₂，……，a_m）＝0の解bをとれば，（b，a₂，……，a_m）は元の方程式の解になる。次にr＝2，m＝2のときを考えてみよう。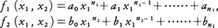と書く。ここで，a_i，b_jはx₂についての多項式である。このようにして，f₁（x₁，x₂），f₂（x₁，x₂）をx₁についての多項式とみなし，上の式に示した終結式，r（f₁，f₂）（x₂）を考える。r（f₁，f₂）（a₂）＝0となるのは，a₀（a₂）＝b₀（a₂）＝0か，f₁（x₁，a₂）＝0，f₂（x₂，a₂）＝0が共通根をもつかのいずれかのときである。いずれの場合にも，ユークリッドの互除法で，f₁（x₁，a₂）とf₂（x₁，a₂）の最大公約式を求めて，f₁（x₁，a₂）＝0，f₂（x₁，a₂）＝0の解が定まる。r（f₁，f₂）（b）≠0ならば，f₁（x₁，x₂）＝f₂（x₁，x₂）＝0の解でx₂＝bとなるものはない。f₁（x₁，x₂）＝0，f₂（x₁，x₂）＝0の解が有限個しかなく，f₁，f₂の次数がn₁，n₂であれば，解の個数はn₁n₂以下である。

　一般の場合には，f_i（x₁，……，x_m），f_j（x₁，……，x_m）のx₁についての終結式r_ij＝r（f_i，f_j）（x₂，……，x_m）をすべてのi，jについて作れば，未知数の数がm－1の場合に帰着する。r＝mのとき，m元連立代数方程式f₁（x₁，……，x_m）＝0，……，f_m（x₁，……，x_m）＝0が有限個の解をもてば，その解の個数は（deg f₁）……（deg f_m）以下である。
→代数方程式
執筆者：丸山 正樹

図－連立方程式

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

連立方程式
れんりつほうていしき

二つ以上の未知数を含む方程式（多元方程式）の組があって、同じ文字が表す未知数は各方程式において同じ値をとるものとするとき、これら方程式の組を連立方程式といい、すべての方程式を同時に成り立たせる未知数の値の組を、連立方程式の解（根(こん)）といい、すべての解（解集合）を求めることを連立方程式を解くという。各方程式が一次であるものを連立一次方程式、各方程式が二次（または一次を含んでよい）であるものを連立二次方程式という。

［竹内芳男］

連立二元一次方程式の解法

　　2x+3y=7……〔1〕
　　3x-4y=2……〔2〕
（1）等置法　〔1〕〔2〕をたとえばxについて解き、それらを等しいと置いて、yの方程式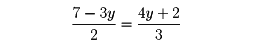

を得る。これを解けばy=1である。この値を〔1〕に代入してx=2が得られる。

（2）代入法（置換法）　〔1〕から得たxの値を〔2〕のxに代入してyの方程式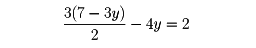

が得られ、これを解いてy=1を得る。

（3）加減法　yの係数をそろえるために〔1〕〔2〕の両辺をそれぞれ4倍、3倍して、辺々を加えると17x=34となり、これからx=2が得られる。

　以上の方法はいずれも一つの未知数を追い出して、他の未知数の方程式をつくることである。これを〔1〕〔2〕から未知数を消去するという（消去法）。一般の連立一次方程式の解法と行列式や行列の理論は密接に関連する。行列式論の起源は、連立一次方程式の解法にあるといわれている。なお連立方程式の解の幾何学的意味や、解の不定、不能については「一次方程式」の項目を参照されたい。

［竹内芳男］

連立二元二次方程式の解法

二元二次方程式の一般形は
　　ax²+bxy+cy²+ex+fy+g=0
である。類型は（a）二次と一次、（b）二次と二次の2種である。（a）の場合は一次方程式から、たとえばxについて解き、これを二次方程式のxに代入すれば、yについての二次方程式が得られる。（b）の場合は（イ）一方の二次方程式の二次式がx、yの一次式に因数分解されるときと、（ロ）どちらも因数分解されないときに分けられる。（イ）の場合は前述の（a）の場合に帰着される。（ロ）の場合は一般的な方法はなく、消去法を用いても四次方程式になり、複雑である。幾何学的には、二つの二次曲線の交点（一般に4点）の座標が解である。方程式のグラフを利用すれば、近似解が得られ、実用的である。

［竹内芳男］

[参照項目] | 一次方程式

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

連立方程式【れんりつほうていしき】

二つ以上の方程式を組にし，それらを同時に満足する未知数または未知関数を求めようとするもの。未知数の数がm個，未知数に関する最高次数がn次の場合をm元n次の連立方程式という。一般にm元の連立方程式は独立の方程式がm個あれば解けるが，m−１個以下では解が無数に存在し，m＋１個以上なら解が存在しない。→方程式

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

連立方程式
れんりつほうていしき
simultaneous equations

2つ以上の未知数を含む2つ以上の方程式の組が与えられ，未知数は与えられた方程式すべてを満足することを要求しているものを，連立方程式という。たとえば，
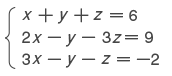は x，y，z を未知数とする連立方程式である。

出典　ブリタニカ国際大百科事典 小項目事典