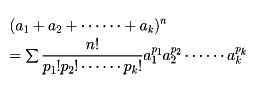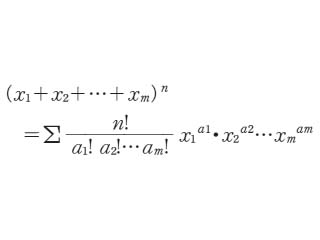関連語
精選版 日本国語大辞典 「多項定理」の意味・読み・例文・類語
たこう‐ていりタカウ‥【多項定理】
改訂新版 世界大百科事典 「多項定理」の意味・わかりやすい解説
多項定理 (たこうていり)
polynomial theorem
k個の文字a1,a2,……,akの和のn乗の展開には次式,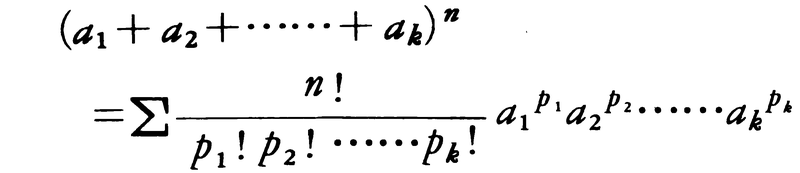
が成立し,これを多項定理といい,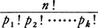 を多項係数と呼ぶ。ただし,Σによる和は,nを負でない整数p1,……,pnの和n=p1+p2+……+pkに分解するすべての場合にわたるものとする。k=2のとき二項定理という。多項定理の応用例を二つあげる。
を多項係数と呼ぶ。ただし,Σによる和は,nを負でない整数p1,……,pnの和n=p1+p2+……+pkに分解するすべての場合にわたるものとする。k=2のとき二項定理という。多項定理の応用例を二つあげる。
例1 n=3,k=3のとき,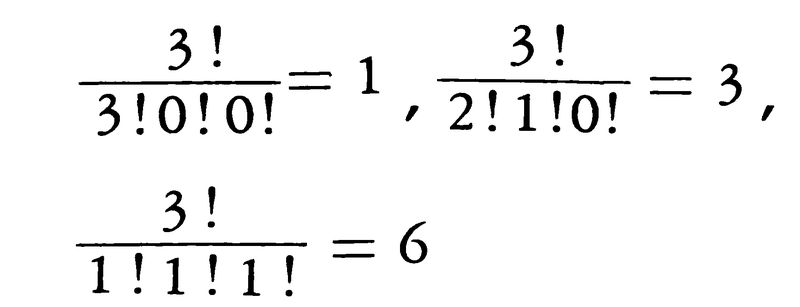
であるから,
(a+b+c)3=a3+b3+c3+3(a2b+a2c+b2a+b2c+c2a+c2b)+6abc
例2 (1+x+x2)6のx4の係数を求める場合には多項定理より,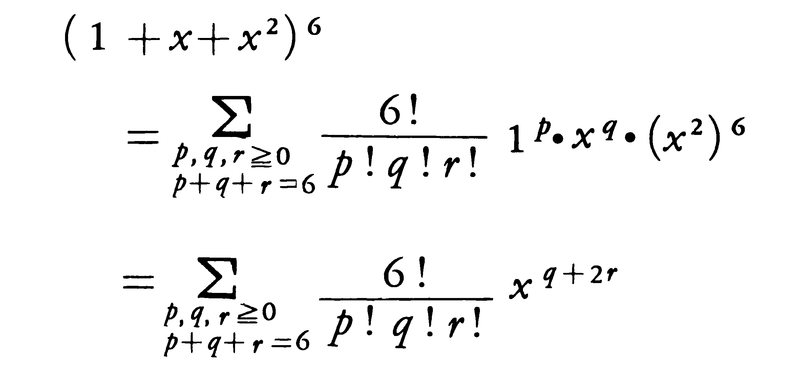
であるから,
を満たすすべての負でない整数p,q,rについての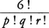 の総和が求める係数である。(2)によりq=0,2,4。それぞれの場合(r,p)=(2,4),(1,3),(0,2)ゆえ,よって求める係数は,
の総和が求める係数である。(2)によりq=0,2,4。それぞれの場合(r,p)=(2,4),(1,3),(0,2)ゆえ,よって求める係数は,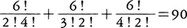
すなわち,x4の係数は90である。
執筆者:杉江 徹
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「多項定理」の意味・わかりやすい解説
法則の辞典 「多項定理」の解説
ブリタニカ国際大百科事典 小項目事典 「多項定理」の意味・わかりやすい解説
多項定理
たこうていり
multinomial theorem
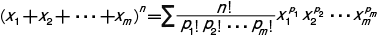 ここで Σ は,p1 ,p2 ,…,pm が正の整数で,p1+p2+…+pm=n という条件を満足するすべての値についての和をつくることを示す。
ここで Σ は,p1 ,p2 ,…,pm が正の整数で,p1+p2+…+pm=n という条件を満足するすべての値についての和をつくることを示す。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「多項定理」の意味・わかりやすい解説
多項定理【たこうていり】
出典 株式会社平凡社百科事典マイペディアについて 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


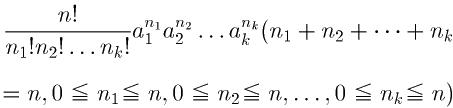 の
の