スターリングの公式 (スターリングのこうしき)
Stirling's formula
自然数nの階乗n!=n・(n-1)・……・2・1を計算するときに用いられる近似式,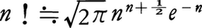 をスターリングの公式という。この近似はnの関数のn→∞のときの極限的な性質をみるため,また近似計算において重要な役割を果たす。近似の程度はnの増加とともによくなる。n=10のとき,10!=3628800で公式による近似は3598600となって,誤差の割合は約0.8%,n=100になると,この割合は0.08%にまで減少し,公式による近似がかなりよいことがわかる。nが大きいとき,二項分布を規格化(平均値を0,分散を1に)したものが標準正規分布に近いことを示すにはこの公式を用いるとよい。またΓ関数Γ(z)において,Γ(n+1)=n!に注意し,|z|が大きいとき近似式,
をスターリングの公式という。この近似はnの関数のn→∞のときの極限的な性質をみるため,また近似計算において重要な役割を果たす。近似の程度はnの増加とともによくなる。n=10のとき,10!=3628800で公式による近似は3598600となって,誤差の割合は約0.8%,n=100になると,この割合は0.08%にまで減少し,公式による近似がかなりよいことがわかる。nが大きいとき,二項分布を規格化(平均値を0,分散を1に)したものが標準正規分布に近いことを示すにはこの公式を用いるとよい。またΓ関数Γ(z)において,Γ(n+1)=n!に注意し,|z|が大きいとき近似式,
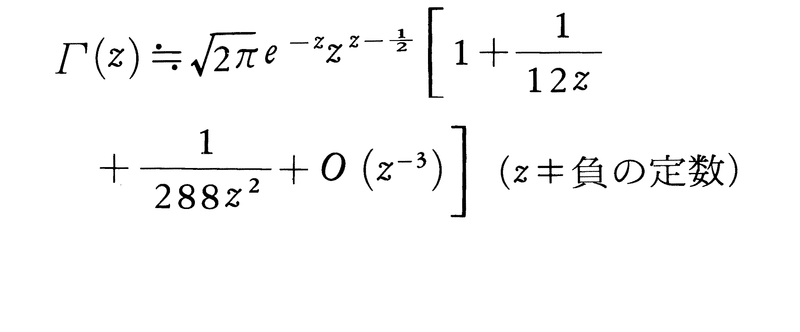
もスターリングの公式と呼ぶことがある。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
スターリングの公式
スターリングのこうしき
Stirling's formula
自然数 n が大きいときの n の階乗 n! の近似値を与える公式で,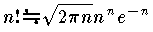 と表わされる。これは,n を非常に大きいとしての近似式で,n→∞ のとき両辺の比が1に近づくことを意味するが,n が小さいときでも,近似の精度は比較的高い。ガンマ関数を使えば,n!=Γ(n+1) であるから上の公式は,
と表わされる。これは,n を非常に大きいとしての近似式で,n→∞ のとき両辺の比が1に近づくことを意味するが,n が小さいときでも,近似の精度は比較的高い。ガンマ関数を使えば,n!=Γ(n+1) であるから上の公式は,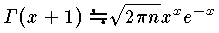 で与えられる。イギリスの数学者 J.スターリングによって発見された。現在ではこの剰余項を n-1 の漸近展開級数で表現した式をもスターリングの公式と呼ぶ。
で与えられる。イギリスの数学者 J.スターリングによって発見された。現在ではこの剰余項を n-1 の漸近展開級数で表現した式をもスターリングの公式と呼ぶ。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
百科事典マイペディア
「スターリングの公式」の意味・わかりやすい解説
スターリングの公式【スターリングのこうしき】
整数nが大きいときその階乗n!について成り立つ近似公式(式1)をいう。n=10のときの誤差は約0.8%で,nが大きいほど誤差は小さい。英国のスターリングJ.Stirling〔1692-1770〕が発見。
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
法則の辞典
「スターリングの公式」の解説
スターリングの公式【Stirling's formula】
大きな整数 n の階乗(n!)を近似的に求めるための公式.通常は第二項までを指している.
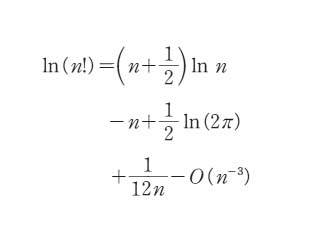
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のスターリングの公式の言及
【階乗】より
…そのほか,テーラー展開,マクローリン展開など,階乗の記号は,数学の多くの公式中にしばしば現れる。n!は,nが大きくなるとき急速に大きくなるが,もちろんnnより小さく,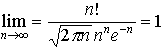 であることが知られている(スターリングの公式)。ここで,πは円周率,eは自然対数の底である。…
であることが知られている(スターリングの公式)。ここで,πは円周率,eは自然対数の底である。…
【ド・モアブル】より
…この間I.ニュートンとの親交は,数学者として大成するのに大いに役だった。彼は,今日スターリングの公式と呼ばれるnが大きいときn!の近似値を与える公式を,定数を除いて確定し,さらに,ベルヌーイ試行,すなわち二項分布が現れる場合の中心極限定理を導いた。これは今日ド・モアブル=ラプラスの定理と呼ばれている。…
※「スターリングの公式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
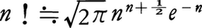 をスターリングの公式という。この近似はnの関数のn→∞のときの極限的な性質をみるため,また近似計算において重要な役割を果たす。近似の程度はnの増加とともによくなる。n=10のとき,10!=3628800で公式による近似は3598600となって,誤差の割合は約0.8%,n=100になると,この割合は0.08%にまで減少し,公式による近似がかなりよいことがわかる。nが大きいとき,二項分布を規格化(平均値を0,分散を1に)したものが標準正規分布に近いことを示すにはこの公式を用いるとよい。またΓ関数Γ(z)において,Γ(n+1)=n!に注意し,|z|が大きいとき近似式,
をスターリングの公式という。この近似はnの関数のn→∞のときの極限的な性質をみるため,また近似計算において重要な役割を果たす。近似の程度はnの増加とともによくなる。n=10のとき,10!=3628800で公式による近似は3598600となって,誤差の割合は約0.8%,n=100になると,この割合は0.08%にまで減少し,公式による近似がかなりよいことがわかる。nが大きいとき,二項分布を規格化(平均値を0,分散を1に)したものが標準正規分布に近いことを示すにはこの公式を用いるとよい。またΓ関数Γ(z)において,Γ(n+1)=n!に注意し,|z|が大きいとき近似式,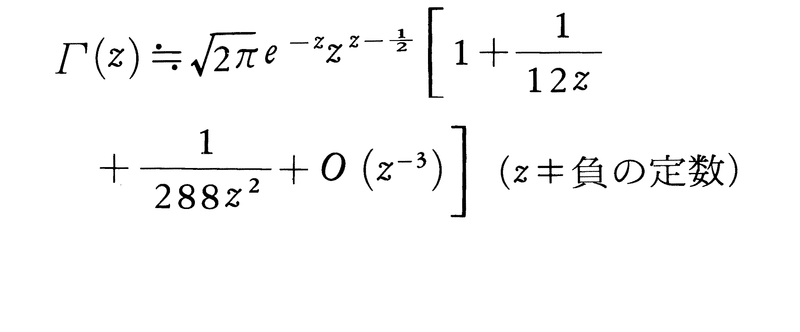


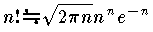 と表わされる。これは,n を非常に大きいとしての近似式で,n→∞ のとき
と表わされる。これは,n を非常に大きいとしての近似式で,n→∞ のとき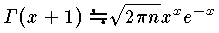 で与えられる。
で与えられる。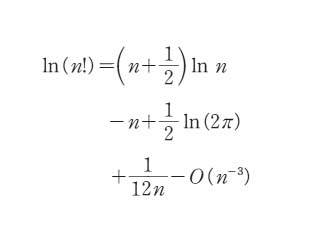
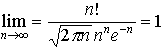 であることが知られている(スターリングの公式)。ここで,πは円周率,eは自然対数の底である。…
であることが知られている(スターリングの公式)。ここで,πは円周率,eは自然対数の底である。…