日本大百科全書(ニッポニカ) 「p進数」の意味・わかりやすい解説
p進数
ぴーしんすう
pを一つの素数とする。riを0≦ri<pのような整数とするとき、無限級数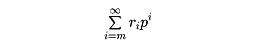
をp進数という。aを正の整数とすると、aは
a=r0+r1p+……+rmpm
(0≦ri<p)
と表されるので、p進数の特別の場合とみることができる。たとえば、p=7のとき、
121=2+17・7=2+(3+2・7)・7
=2+3・7+2・72
負の整数を有限和で表すことはできない。しかし、無限級数の形に表そうとするなら、それは可能である。たとえば、
-3=4+(-1)・7
=4+6・7+(-1)・72
=4+6・7+6・72+6・73+……
分母bがpで割り切れない分数1/bも、無限級数の形にすることができる。たとえば、
1=4・2+(-1)・7=4・2+4・5・7+(-3)・72
=4{2+5・7+1・72+(-1)・73}=……
となるから、
1/4=2+5・7+1・72+……
これは右辺をr0+r1p+r2p2+……と置き、順にr0、r1、……を定めてもよい。
一般に有理数は
a=ps(r0+r1p+r2p2+……)
と無限級数で表される。この右辺の形の無限級数をp進数というのである。有理数はp進数であるが、p進数は有理数を表すとは限らない。p進数の全体は可換体をつくり、これをp進体という。整数論の研究のために考え出されたものである。
[寺田文行]