翻訳|algebra
精選版 日本国語大辞典 「代数学」の意味・読み・例文・類語
だいすう‐がく【代数学】
日本大百科全書(ニッポニカ) 「代数学」の意味・わかりやすい解説
代数学
だいすうがく
algebra
幾何学、解析学と並ぶ数学の大きな分野の一つで、数の四則のような演算が定義された集合をおもな研究対象にしている。より正確にいえば次のようになる。集合AとA自身との積集合A×AからAへの写像
f:A×A∋(a,b)→f(a,b)∈A
をAの二項演算という。数の足し算(a,b)→a+bおよび掛け算(a,b)→abは、数の集合の二項演算である。
有限個の二項演算が定義されている集合を代数系という。現代の代数学は、ひとことでいえば、代数系を研究する数学である。とくに重要な代数系として、群、環、体、リー環があり、それぞれに独自の理論ができているが、相互の代数系を関係づけた研究もなされ、また、他の数学の分野への応用も考えられてきている。
[菅野恒雄]
群論
整数全体の集合Zでは、数の足し算と引き算の二つの二項演算ができる。一方0以外の有理数全体の集合Qxでは、数の掛け算と割り算ができる。これら二つの代数系Z、Qxは集合としても違うし、その二項演算もまったく異なるが共通の性質をもっている。それが群という考え方である。つまり、集合Gに
f:G×G∋(a,b)→f(a,b)∈G
なる二項演算が定義され
①f(f(a,b),c)=f(a,f(b,c))
(a,b,c∈G)
②Gに特殊な元eがあって
f(a,e)=f(e,a)=a (a∈G)
③写像G∋a→g(a)∈Gが定義され
f(a,g(a))=f(g(a),a)=e
(a∈G)
を満たすとき、Gを群という。
さて、群をこのように定義すると、Z、Qxのような数の群以外の群があることがわかる。たとえば、Mを空でない集合とし、P(M)をMからMの上への一対一写像全体とする。P(M)の元σ、μに対し、
④(μ゜σ)(m)=μ(σ(m))
(m∈M)
とすると、μ゜σはP(M)の元で、二項演算(μ,σ)→μ゜σでP(M)は群になる。この群P(M)をMの変換群といい、P(M)の元をMの置換という。とくにM={1,2,……,n}のとき、P(M)をSnと書き、n次の対称群という。Snはn!個の元からなっている。一般に元の個数が有限である群を有限群というが、対称群Snは有限群論でとくに重要な役をする。
また、Mが線形空間のとき、P(M)の元σで線形写像になっているもの全体の集合GL(M)は、それ自身、群になる。この群GL(M)は、線形空間の次元をnとすると、n次正方行列で行列式が0でないもの全体のつくる乗法群と本質的に同じで、線形空間Mの自己同形群という。
群を研究する数学が群論であるが、とくに
f(a,b)=f(b,a) (a,b∈G)
が成り立つ群を可換群またはアーベル群といい、数学の他の分野に広く応用されている。置換群は、Mの元が3個以上なら可換群ではないが、幾何学などと関連が深い。
[菅野恒雄]
環論
整数全体Zは、足し算、引き算のほかに掛け算もできる。このように集合Aが
⑤A×A∋(a,b)→a+b∈Aで可換群になる。
⑥A×A∋(a,b)→ab∈Aについて、
(ab)c=a(bc) (a,b,c∈A)
さらに、特殊な元eで
ae=ea=a (a∈A)
なるものがある。
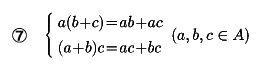
を満たすとき、Aを環という。環は、足し算、引き算、掛け算の三つの二項演算をもつ代数系である。環Aでは⑤からa+b=b+a (a,b∈A)が成り立つ。積について、とくに
⑧ab=ba (a,b∈A)
が成り立つとき、Aを可換環という。Zや多項式全体C[X]は可換環である。n次正方行列全体Mn(C)は、行列の加法、乗法で環になるが、n≧2なら可換環でない。環Mn(C)は、C上の線形空間でもあり、スカラー積と、環としての乗法の間に
⑨α(ab)=(αa)b=a(αb)
(α∈C, a,b∈Mn(C))
が成り立つ。このように、環でもあり線形空間でもあるAが⑨を満たすとき、Aを多元環という。環を研究する数学が環論である。とくに可換環と多元環は古くから研究されている。
[菅野恒雄]
体論
有理数全体Qは、足し算、引き算、掛け算ができて、可換環であるが、さらに0以外の元による割り算ができる。このように集合Kが
⑩Kは加法と乗法で可換環である。
⑪Kの0以外の元全体Kxは乗法で群である。を満たすとき、Kを体という。
Qと同様に、実数全体R、複素数全体Cは体であるが、Zは体でない環である。体は、環の特別なもので、俗に、四則演算が可能な代数系といわれるが、四則のうちの割り算、(a,b)→ab-1はb≠0のとき可能であるから、厳密にいうとKの二項演算ではない。条件⑪でKxが可換群になるとき、Kを可換体という。可換体でない体を非可換体といい、可換体を単に体ということもある。QはCに含まれる最小の体であるが、QとCの間に無数の体がある。このような体を数体という。
Q係数のn≧一次多項式f(X)は、代数学の基本定理により、最高次の係数を1とすると、
⑫ f(X)=(X-ω1)(X-ω2)
……(X-ωn)
のように、f(X)の根といわれる複素数ω1、……、ωnで書ける。このようなf(X)の根になっている複素数ωを代数的数という。代数的数全体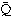 はQとCの間にある体で、
はQとCの間にある体で、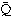 を研究する数学が整数論である。
を研究する数学が整数論である。
さて、⑫のf(X)の根ω1、……、ωnとQを含む最小の体Q(ω1,……,ωn)は、n個の数ω1、……、ωnとQの元から有限回の四則演算で得られる数全体からなるが、体Q(ω1,……,ωn)を集合と考えての置換σでQ(ω1,……,ωn)の元a、bに対し
σ(a+b)=σ(a)+σ(b),
σ(ab)=σ(a)σ(b)
を満たすもの全体は、二項演算④で有限群Gをつくる。さらに、Q(ω1,……,ωn)に含まれる体と、Gに含まれる群との間に、自然で美しい対応がつくことがわかっている。これが、現代代数学の一つの頂点であるガロアの定理である。
代数的数でない数を超越数という。数体Kが超越数を含むとき、KをQの超越拡大体という。この種の体は、代数多様体の関数体として現れ、代数幾何学で重要である。
[菅野恒雄]
リー環
環の公理⑤が成り立ち、さらに⑥のかわりに一種の乗法(a,b)→[a,b]について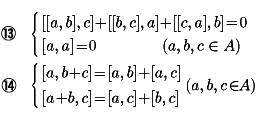
が成り立つ代数系Aをリー環という。
n次正方行列全体Mn(C)は、行列の加法と乗法で環であったが、行列の加法と、新しい乗法[a,b]=ab-baでリー環にもなっている。群と多様体の結合概念にリー群といわれるものがあるが、この群の単位元での接空間は自然な方法でリー環になる。このように、リー環は多様体と結び付き、重要である。
[菅野恒雄]
代数学の歴史
数を記号で表すことが代数学の始まりなら、それは紀元前インド、アラビア、エジプトなどで行われていた。16世紀ヨーロッパで記号法が完成し、すでに得られていた一次方程式、二次方程式に次いで、カルダーノの三次方程式、フェラリの四次方程式の解法の発見がある。その後、五次以上の方程式の代数的解法の研究がなされたが、19世紀に入り、アーベル、ガロアらによって、次数が五以上の代数方程式は一般には代数的に解けないことが証明された。この根拠に、いわゆるガロアの理論がある。この理論の整理とフェルマーの問題などの研究が契機となり、群、環、体の基礎理論が確立された。
また、角の三等分など、古い幾何学の問題が代数の理論で証明されるなど、幾何学、解析学に応用される一方、公理を用いたさまざまな代数系が考え出され、今日の抽象代数学ができあがった。
[菅野恒雄]
『彌永昌吉・布川正巳編『代数学』(1968・岩波書店)』▽『石田信著『代数学入門』(1978・実教出版)』
改訂新版 世界大百科事典 「代数学」の意味・わかりやすい解説
代数学 (だいすうがく)
algebra
西欧語algebraの語源は,アラビアの数学者フワーリズミーの著書《ジャブルとムカーバラの算法の摘要の書al-Kitāb al-mukhtasarfi hisāb al-jabr wa-al-muqābalah》の一部アルジャブルal-jabr(変形,移項などを意味する)である。
広い意味での代数学は,(1)代数方程式の解法および連立方程式の解法に関連する事項を中心とする古典代数学,(2)抽象的な体論,群論,環論などを中心とする抽象代数学,(3)整数論や代数幾何学などのうち,研究方法が(2)の方法と深い関連をもつ分野を含むが,ここでは,(1),(2)について述べる。
古典代数学の歴史
東洋では中国において紀元前にすでに負の数を用い,連立一次方程式の解法を知っていた。西洋では前2千年紀前半のバビロニアで二次方程式の解法が知られていた(ただし,負の数,負の根は考えられなかった。このことは西洋では16世紀まで続く)。ギリシアでは,前3,4世紀には二次方程式を作図によって解いたが,1世紀になって計算によって解くようになった。3世紀ころには不定方程式も現れた。インドでは6世紀ころに二次方程式の解法が見いだされたようである。これらの古代の古典代数学のその後の発展は緩やかであり,中国において,13世紀に高次方程式の数値解法が行われたが,16世紀の西洋において急速な進展が始まった。その第1はフェロScipione del Ferro(1465-1526)らによる三次方程式の解法,続いてL.フェラリによる四次方程式の解法の発見である。第2はF.ビエトらによる数式表示の革命,すなわち,それまで方程式は文章で表されていたのであるが,まずドイツで+,-の記号の使用が始まり,ビエトは+,-だけでなく,未知数を母音を表す文字で,係数を子音を表す文字で表して,文字係数の一般方程式を書き始めた。一方,三次方程式のG.カルダーノの解法においては,実根を求めるのに虚数が必要になることが当時の数学者を悩ませたが,18世紀のL.オイラーらが計算に虚数を使うようになり,やがて18世紀末から19世紀にかけてC.F.ガウスが複素数の重要性を明確にとらえて,ガウス平面の利用を含めて複素数を実在の数として数学者に意識させるようにした。ガウスを含む何人かの人々により複素数の体系が確立したことは,その後の数学の発展に非常に大きい貢献をした。
高次方程式の解法究明の過程でガロアの理論が生まれ,群の概念を生じ,さらに抽象的な体,環が定義されて抽象代数学の発生へと進んだのは19世紀後半から20世紀前半にかけてのことである。
古典代数学の対象
古典代数学は,一つまたは多くの未知数の間の加減乗除による関係式から未知数の値を求めること,すなわち,代数方程式あるいは多元連立方程式を解くことにその中心がある。したがって,次のことも対象に含まれる。
(1)消去法 与えられた連立方程式のなかから二つの式を選び,それを一つの未知数xについて整理したものをf,gとして,その終結式R(f,g)を考えると,x以外の未知数についての関係式R(f,g)=0が得られる。すなわち,xの消去である。式が多くあるときは,f,gをいろいろとりかえてこのような関係式を作ることも必要である。
(2)実根の数 次に紹介するステュルムの定理Sturm's theoremが有名である。実数係数の多項式f(x)=a0xn+a1xn⁻1+……+an(a0≠0)に対して,f0(x)=f(x),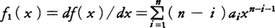 と定め,i≧1に対し,fi-1(x)をfi(x)で割った余り(次数はfi(x)の次数より小)に-1を掛けたものをfi+1(x)と定める。ただし,余りが0ならfi+1を作らずにfiを最後のものとする。これによってできた列がf0(x),f1(x),……,fs(x)であれば,次のことがいえる。f(b)≠0,f(c)≠0,b<cのとき,f(x)=0の実数解でbとcとの間にあるものの数(互いに異なるものの数であって,重根があっても重複度は数えない)はVb-Vcに等しい。ここに,各実数zに対しVzは,列f0(z),f1(z),……,fs(z)において,まず0であるところを消してしまい,その上で,この列で正から負,または負から正に変わる個所の数である(例えば,列が1,1,0,1,0,-1なら,Vz=1)。
と定め,i≧1に対し,fi-1(x)をfi(x)で割った余り(次数はfi(x)の次数より小)に-1を掛けたものをfi+1(x)と定める。ただし,余りが0ならfi+1を作らずにfiを最後のものとする。これによってできた列がf0(x),f1(x),……,fs(x)であれば,次のことがいえる。f(b)≠0,f(c)≠0,b<cのとき,f(x)=0の実数解でbとcとの間にあるものの数(互いに異なるものの数であって,重根があっても重複度は数えない)はVb-Vcに等しい。ここに,各実数zに対しVzは,列f0(z),f1(z),……,fs(z)において,まず0であるところを消してしまい,その上で,この列で正から負,または負から正に変わる個所の数である(例えば,列が1,1,0,1,0,-1なら,Vz=1)。
(3)対称式,交代式 方程式の根と係数の関係によって,xn+a1xn⁻1+……+anの根α1,α2,……,αnをとると,-a1,a2,……,(-1)rar,……,(-1)nanがα1,α2,……,αnの基本対称式であり,根の差積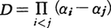 はα1,α2,……,αnの交代式であるから,対称式,交代式の理論は方程式論と縁が深い。
はα1,α2,……,αnの交代式であるから,対称式,交代式の理論は方程式論と縁が深い。
抽象代数学
重要な対象は群,環,体であるが,もっと一般に,演算の与えられた集合はすべて抽象代数学の対象でありうる。その演算の性質に応じて重要度や意義が異なるわけであり,このような集合を総称して代数系というが,抽象代数学で群,環,体に次いで重要視されているものは半群semigroupであり,それは次のように定義される。乗法をもつ集合Sが半群であるとは,その乗法が結合法則a(bc)=(ab)cを満たすときにいう。これは群よりだいぶ弱い条件である。リー環と呼ばれる代数系はリー群論と密接な関連をもつもので,結合法則は仮定されていないので,通常,環論というときの環には含まれない。
抽象代数学の発生は,五次以上の代数方程式の解法の探究のため,根の置換のなす群,すなわち現在,ガロア群と呼ばれるものの考察に始まるといえる。そのようにしてできたガロアの理論は,一つの方程式の根全体で生成された体と,その自己同型のなす群とを考えることになり,置換群に発展し,やがて抽象的な群の定義がなされ,それは合同変換群など幾何学的な群を考えることにもつながって発展した。また,ガロアの理論で芽生えた体の概念は,E.スタイニッツの抽象的体論(1910)に至って抽象代数学の重要な分野となった。他方,一つの代数数体の中の代数的整数全体がもつ乗法と加法という二つの演算を抽象化して環の概念が生まれた。代数的整数全体のなす環では,一般には素元分解の一意性が成り立たないため,E.E.クンマーが理想数を考え,J.W.R.デデキントはそれがイデアルで実現されることを見いだした。このようにして導入されたイデアルは一般の環にも適用され,園正造(1886-1969)およびA.E.ネーターが独立にイデアル論の建設を始めた。とくにネーターの貢献は大きく,その後の環論(イデアル論,加群の理論を含む)は抽象代数学の最重要分野と見なされるほどに発展した。扱う環が可換であるかどうかは,取扱上差があるだけでなく,応用も異なるので,可換環論と非可換環論とはだいぶ違った発展をしてきた。前者はとくに代数幾何学と密接した発展をし,後者は行列環や,群の表現などに関連した重要部分をもっている。近年,トポロジーにおける代数的手法を抽象化して加群を研究する分野が発達してきた。この分野はホモロジー代数と呼ばれている。
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「代数学」の意味・わかりやすい解説
代数学【だいすうがく】
→関連項目算数|抽象代数学|フワーリズミー
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「代数学」の意味・わかりやすい解説
代数学
だいすうがく
algebra
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の代数学の言及
【多元環】より
…実数を係数とする二次の正方行列全体をAで,また実数全体をKで表すと,次の(1)(2)が成り立っている。(1)AはK上の加群である。すなわち,Aの二つの元の和が定義されていて,それについてAはアーベル群(可換群)であり,Kの元λとAの元aの積λa(スカラー倍)が定まっていて次の(イ)~(ハ)の性質をもつ。 (イ)λ(a+b)=λa+λb (ロ)λ1(λ2a)=(λ1λ2)a (ハ)1・a=a(2)Aの二つの元a,bの積abが定義されていて,(イ)~(ニ)の性質をもつ。…
【フワーリズミー】より
…アラビア代数学の出発点をつくった数学者で,また天文学者,地理学者。アラル海の南ホラズムの出身で,アッバース朝のカリフ,マームーン治下のバグダードで活躍した。…
※「代数学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

