精選版 日本国語大辞典 「整数論」の意味・読み・例文・類語
せいすう‐ろん【整数論】
- 〘 名詞 〙 整数のもつ、一般の実数にない性質(約数・倍数・素数など)を研究対象とする数学の一分科。数論。
改訂新版 世界大百科事典 「整数論」の意味・わかりやすい解説
整数論 (せいすうろん)
number theory
数論ともいう。整数のもつ特殊な性質は古くから人々の興味を引いてきた。整数論は,それらの整数の性質についての研究から始まるが,後に理論の発展とともに研究対象も広がっていった。この項目では,前半において整数の整除,合同などに関する初等的理論である初等整数論について述べ,後半で整数論の歴史を述べる。
初等整数論
整除
二つの整数a,b(b≠0)に対して,
a=qb+r (0≦r<|b|,|b|はbの絶対値)
を満たす整数q,rがただひととおりに定まる。qを商,rを剰余という。r=0であるとき,aはbで整除される,または割り切れるといい,aはbの倍数,bはaの約数であるという。
素数
1以外の正の整数pで,1と自分自身以外に正の約数をもたないものを素数という。2以外の素数は奇数なので奇素数という。1と自分自身の絶対値以外に正の約数をもつ整数を合成数という。二つの整数a,bの積が素数pで割り切れるならば,aまたはbの少なくとも一方はpで割り切れる。また0,±1以外の整数aは,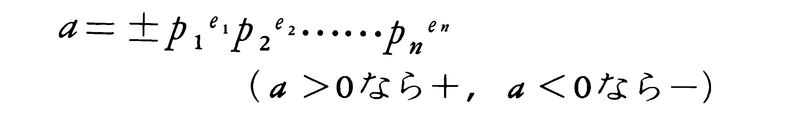
と,素数の積にただひととおりに素因数分解できる。
完全数,親和数
正の整数aに対して,aのすべての正の約数の和をs(a)で表すことにする。例えば,s(6)=1+2+3+6=12である。s(a)>2a,s(a)=2a,s(a)<2aの三つの場合に従って,aは豊数(過剰数),完全数,輸数(不足数)であるという。ユークリッドは,2e-1が素数であれば2e⁻1(2e-1)は完全数であることを示したが,L.オイラーは偶数の完全数はこの形に限ることを示した。奇数の完全数は,いまのところ一つも知られていない。
二つの正の整数a,bに対し,a以外のaの約数の和がbであり,b以外のbの約数の和がaであるとき,すなわち,s(a)=s(b)=a+bであるときaとbは互いに友数,または親和数であるという。例えば,220と284,17296と18416は親和数である。9世紀のアラビアの数学者サービト・ブン・クッラは,h=3・2n-1,t=3・2n⁻1-1,s=9・22n⁻1-1が奇素数ならば,2nhtと2nsは親和数であるという結果を得ている。上の二つの例はそれぞれn=2,4の場合である。その後もいろいろの方法で多くの親和数が見いだされている。
合同
整数a,bの差が整数mで割り切れるとき,aとbはmを法として合同であるといい,これを,
a≡b (mod m)
で表す。例えば,3≡10 (mod 7)である。整数mに対し,aとbがmを法として合同であるとき同じ組に属するとして,整数全体をm個の組に分けることができる。その組をmを法とする剰余類という。剰余類の中で,法mと互いに素な整数からなる類を既約剰余類という。法mの既約剰余類の個数をφ(m)で表し,φをオイラーの関数という。ただし,φ(1)=1と定める。互いに素な正の整数m,nに対し,φは,
φ(mn)=φ(m)φ(n)
を満たし,mの素因数分解が,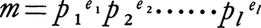 であるとき,φ(m)は,
であるとき,φ(m)は,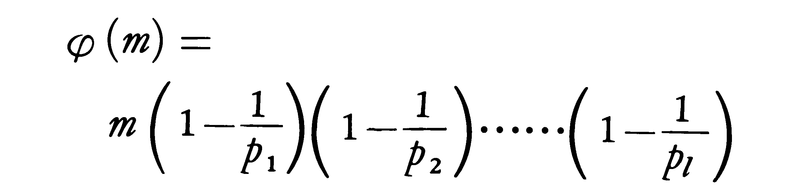
で与えられる。また1,2,……,nの中に,nの正の約数dに対し,nとの最大公約数がdになるものはφ(n/d)個存在し,したがって,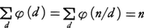 という式が得られる。ここで,dはnの正の約数全体にわたる。
という式が得られる。ここで,dはnの正の約数全体にわたる。
原始根
法mが素数pであるとする。このとき,pと互いに素な整数aに対し,
ap⁻1≡1 (mod p)
が成り立つ。これはフェルマーの定理と呼ばれている。p-1より小さい正の整数kに対しては,akと1がpを法として合同にならないとき,aはpを法としての原始根,またはpの原始根という。p=7に対しては3と5,p=11に対しては2,6,7,8が原始根である。原始根を含む類の個数は,オイラーの関数を用いてφ(p-1)で与えられる。
rがpの一つの原始根であれば,1,r,r2,……,rp⁻2は,どの二つも互いに合同ではなく,これらが既約剰余類の代表系を与えており,したがってpと互いに素な整数aに対して,
a≡rα (mod p) (0≦α<p-1)
を満たす整数αがただ一つだけ定まる。このことをrを底とするaの指数といい,Indr(a)で表す。p=11のとき,rとして2をとると,Indr(a)は次の表のようになる。 Indrはpと互いに素な整数a,bに対し,
Indrはpと互いに素な整数a,bに対し,
Indr(ab)≡Indr(a)+Indr(b)
(mod p-1)
を満たす。この性質を用いると合同式,
3x≡5 (mod 11)
は,次のようにして解ける。前式から,
Ind2(3)+Ind2(x)≡Ind2(5) (mod 10)
前の表から,Ind2(3)=8,Ind2(5)=4だから,Ind2(x)=6を得,再び表から,
x≡9 (mod 11)
が得られる。
また素数pに対し,
1・2・……・(p-1)≡-1 (mod p)
が成り立つ。これはウィルソンWilsonの定理と呼ばれている。
整数論的関数
自然数に対して定義された複素数に値をとる関数を整数論的関数という。整数論的関数fが,(1)f(1)=1,(2)m,nが互いに素ならばf(mn)=f(m)f(n)を満たすとき,乗法的であるという。約数の和s(m)やオイラーの関数φは乗法的な整数論的関数の例である。fが整数論的関数であるとき,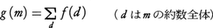 で定められるgも整数論的関数である。fが乗法的ならば,gも乗法的である。逆に次のように定めるメービウスの関数μを用いると,gを用いてfを表すことができる。すなわちμを,(1)μ(1)=1,(2)mがある素数の平方で割り切れるときはμ(m)=0,(3)m=p1・p2・……・pk(p1,……,pkは相異なる素数)のときはμ(m)=(-1)kと定める。μは乗法的な整数論的関数で,mが1でなければ,
で定められるgも整数論的関数である。fが乗法的ならば,gも乗法的である。逆に次のように定めるメービウスの関数μを用いると,gを用いてfを表すことができる。すなわちμを,(1)μ(1)=1,(2)mがある素数の平方で割り切れるときはμ(m)=0,(3)m=p1・p2・……・pk(p1,……,pkは相異なる素数)のときはμ(m)=(-1)kと定める。μは乗法的な整数論的関数で,mが1でなければ,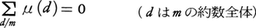 である。μを用いると,fは,
である。μを用いると,fは,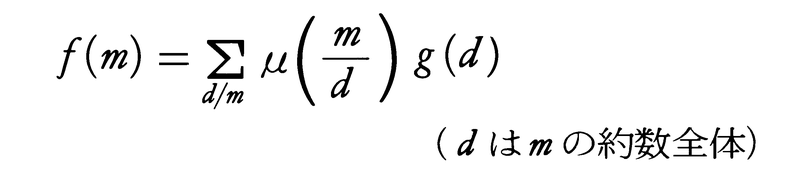
と表される。これをメービウスの反転公式という。
平方剰余
pを奇素数とする。一次の合同式,
ax≡b (mod p)
は,aとpが互いに素ならばいつも解をもつが,二次以上の合同式は必ずしも解をもたない。整数aに対し合同式,
x2≡a (mod p)
が解をもつときaはpの平方剰余,もたないとき平方非剰余であるという。pと互いに素な整数aはその指数Indr(a)が偶数のとき平方剰余,奇数のとき平方非剰余である。p=11に対して1,3,4,5,9は平方剰余であり,2,6,7,8,10は平方非剰余である。またこのことからp-1個の既約剰余類のうちの半分の剰余類に属するものは平方剰余で,残りの半分の剰余類に属するものは平方非剰余であることがわかる。pと互いに素な整数aが,平方剰余であるか,平方非剰余であるかに従って,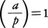 または,
または,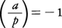 と定め,これをルジャンドル記号という。これに対し,オイラーの規準と呼ばれる次の式,
と定め,これをルジャンドル記号という。これに対し,オイラーの規準と呼ばれる次の式,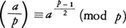 が成り立つ。これからpと互いに素な整数a,bに対し,
が成り立つ。これからpと互いに素な整数a,bに対し,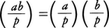 が成り立つことがわかる。また次の関係式は平方剰余の相互法則と呼ばれ,非常に基本的である。すなわち,相異なる奇素数p,qに対し,
が成り立つことがわかる。また次の関係式は平方剰余の相互法則と呼ばれ,非常に基本的である。すなわち,相異なる奇素数p,qに対し,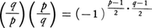 また,奇素数pに対し,
また,奇素数pに対し,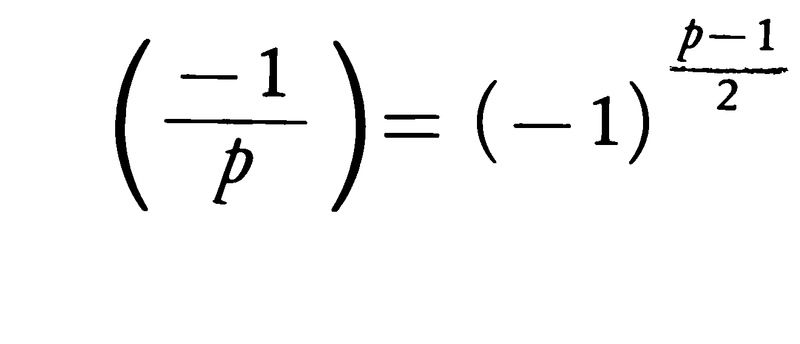
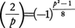 が成り立つ。これらはそれぞれ,平方剰余の相互法則の第1補充法則,第2補充法則と呼ばれている。
が成り立つ。これらはそれぞれ,平方剰余の相互法則の第1補充法則,第2補充法則と呼ばれている。
整数論の歴史
整数論は古代ギリシアに始まる。ユークリッドは《ストイケイア》の中で,整数の素因数分解が一意的であることや,素数が無限に存在すること,ユークリッドの互除法と呼ばれる二つの整数の最大公約数を求める方法など,整数の簡単な性質について述べている。3世紀ころには,アレクサンドリアの数学者ディオファントスが不定方程式に関する多くの問題を考察した。例えば,
ax2+bx+c=y2 (a,b,cは整数)
という形の不定方程式について,いくつかの場合に解を得ている。中国でも1世紀ころには,今日の言葉でいうと互いにどの二つも素な整数m1,m2,……,mnと整数r1,……,rnに対し合同式,
x≡r1(mod m1),x≡r2 (mod m2),……,x≡rn(mod mn)
を満たすxを求める方法が知られていた。インドでは7世紀ころに,ブラフマグプタが初めて二元一次不定方程式,
ax+by=c (a,b,cは整数)
の一般的解法を与え,12世紀ころにはバースカラがペル方程式を解く方法を得た。
17世紀に入ると,フランスにP.deフェルマーが現れ,中世において停滞していた整数論の研究を復興し,これが近代の整数論の出発点となった。フェルマーはディオファントスの著書から,とくに不定方程式に興味をもち,多くの結果をたいていの場合証明なしに書き残した。また,フェルマーの定理や,p≡1 (mod 4)の素数は必ずm2+n2(m,nは整数)の形に表されるなどの結果も得ている。
18世紀には,L.オイラーがフェルマーの述べた命題の多くに証明を与え,さらに多くの重要な結果を残した。その一つは平方剰余の相互法則の発見である。整数Nに対し素数pが,p=m2+Nn2と表されたとすると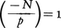 であるが,では〈
であるが,では〈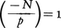 となる素数はどのようなものであろうか?〉。このような疑問からオイラーは平方剰余の相互法則を発見した。この平方剰余の相互法則は,その後A.M.ルジャンドルによって再発見され,特別な場合の証明が与えられたが,完全な証明はC.F.ガウスが初めて与えた。またオイラーは,関数
となる素数はどのようなものであろうか?〉。このような疑問からオイラーは平方剰余の相互法則を発見した。この平方剰余の相互法則は,その後A.M.ルジャンドルによって再発見され,特別な場合の証明が与えられたが,完全な証明はC.F.ガウスが初めて与えた。またオイラーは,関数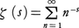 を考え,ζ(s)についていくつかの重要な性質を見いだした。この関数は19世紀になって素数定理との関係からG.F.リーマンによって研究され,リーマンのゼータ関数と呼ばれている。またオイラーの始めた楕円積分の研究は,19世紀に入って,ガウス,N.H.アーベル,C.G.J.ヤコビ,F.G.アイゼンシュタイン,L.クロネッカーらにより発展し,整数論と深く関係していることが明らかにされてきた。18世紀には,オイラー以外にもJ.L.ラグランジュ,ルジャンドルらが,不定方程式や連分数の理論を中心に研究した。ルジャンドルは,それまでに知られていた整数論の結果を《Essai sur la théorie de nombre》という著書にまとめたが,この書名から整数論という名称がでてきた。
を考え,ζ(s)についていくつかの重要な性質を見いだした。この関数は19世紀になって素数定理との関係からG.F.リーマンによって研究され,リーマンのゼータ関数と呼ばれている。またオイラーの始めた楕円積分の研究は,19世紀に入って,ガウス,N.H.アーベル,C.G.J.ヤコビ,F.G.アイゼンシュタイン,L.クロネッカーらにより発展し,整数論と深く関係していることが明らかにされてきた。18世紀には,オイラー以外にもJ.L.ラグランジュ,ルジャンドルらが,不定方程式や連分数の理論を中心に研究した。ルジャンドルは,それまでに知られていた整数論の結果を《Essai sur la théorie de nombre》という著書にまとめたが,この書名から整数論という名称がでてきた。
1801年にはガウスの《数論研究Disquisitiones arithmeticae》が出版され,整数論は,それ以前の知識の集積という状態から体系的な数学の一分野になった。この著書においてガウスは,初等整数論の結果を系統立てて述べた後,平方剰余の相互法則の一般的な証明を与え,二変数二次形式論を展開して,その二次の不定方程式への応用を述べ,最終章においては円分方程式xn-1=0について論じ,2n+1の形の素数に対しては,正p角形で作図可能であることを述べている。ガウスはとくに平方剰余の相互法則に興味をもち,それぞれ異なった着想に基づく証明を全部で六つ与えた。
その後ガウスは4乗剰余の相互法則の研究を始め,そのためにガウス数体と呼ばれる二次体の整数論を展開した。これが代数体の整数論の出発点となった。この4乗剰余の相互法則の研究は,一般のnべき剰余の相互法則の研究として,アイゼンシュタイン,E.E.クンマーらに受け継がれ,さらにD.ヒルベルトによる類体論の構想の中に組み入れられた。
P.G.L.ディリクレは当時,難解であったガウスの《数論研究》の内容を理解しやすいものにしようと努め,さらに整数論に重要な寄与をした。その一つは解析学を整数論に応用したことである。ディリクレはこの解析学を用いる方法で算術級数の定理の証明を与えた。ディリクレの方法を発展させていく中から解析的整数論ができてきた。ディリクレに引き続いて現れたクンマーは,フェルマーの大定理の研究から出発して,xn-1=0の根で生成される円分体を詳しく研究した。この体では,素因数分解の一意性が成り立たず,これが研究を困難にしていたが,クンマーは理想数というものを考えてこれを克服した。この理想数の考えは,J.W.R.デデキントにより簡明なイデアルの理論としてまとめられ,その後の代数体の整数論の発展に重要な役割を果たした。クンマーの弟子であったクロネッカーは代数体の整数論に寄与するとともに,楕円関数論と整数論の関連を研究し,これについて〈青春の夢〉と呼ばれる予想を提出した。これは類体論の完成とともに解決されるが,これを一般化した問題は,20世紀に入ってもヘッケE.Hecke(1887-1947)らによって研究され,重要な研究対象の一つになっている。19世紀の終りころに,ヒルベルトはドイツ数学会への整数論に関する報告《数論報告Zahlbericht》において,それまでに得られていた代数的整数論に関する結果を統一的な形で展開し,さらにその数年後には,その後の代数的整数論の発展に重要な影響を与えた類体論の構想を発表した。これは1920年ころに高木貞治により証明が与えられたが,E.アルティン,H.ハッセ,C.シュバレーらの研究によりさらに深い理論になっていった。
20世紀に入って,代数幾何学などが整数論における重要な方法として取り入れられ,整数論の扱う対象はますます多様なものになってきている。
→解析的整数論 →代数体の整数論 →二次体の整数論
執筆者:斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「整数論」の意味・わかりやすい解説
整数論
せいすうろん
整数についての研究を対象とする数学の学問領域。
古代の整数論
不定方程式x2+y2=z2の自然数解をピタゴラス数という。すべてのピタゴラス数を求める方法が、ピタゴラスをはるかにさかのぼる紀元前2000年近いころにバビロニアで知られていたことを推測させる十分な証拠がある。そのことはまた、数学が、かなり早い時期から実用を離れた知的探究の対象となっていたことをも意味するであろう。
ギリシア数学の総決算ともいえるユークリッドの『ストイケイア』の第7巻から第9巻には整数論が扱われている。そのなかでも有名な命題をいくつか拾ってみる。
(1)素因数分解とその一意性。
(2)ユークリッドの互除法 最大公約数を求める計算法。
(3)ユークリッドの素数定理 素数の個数には限りがないことの背理法による証明。
(4)2n-1が素数ならばa=2n-1(2n-1)は完全数、つまりaの約数の和が2aである。
この(4)の逆、すなわち偶数の完全数が前記の形に表せることは、のちにオイラーによって証明された。奇数の完全数の存在はまだ知られていない。なお、幾何学的色彩の強いギリシア数学のなかでディオファントスの『数論』を落とすことはできない。不定方程式の有理数解を扱ったこととともに、未知数を文字で表したことも重要な業績である。
[足立恒雄]
近世の整数論
中世ヨーロッパにおいては整数論は学問としての体裁を整えなかったが、アラビアにおいてギリシアの古典が保存され、一定の研究がなされていた。文芸復興期以後ギリシア古典のラテン語への翻訳がされるようになったが、そのなかに、長らく埋もれていたディオファントスの『算術』のバシェClaude Gaspard Bachet de Méziriac(1581―1638)による翻訳があった。フェルマーは確率論の始祖、解析幾何的手法の研究者として知られるが、なかでも他の同時代の人たち(パスカル、デカルトら)と際だった対照をみせるのは、整数論に対する格別の愛好であり、したがってフェルマーは近代的整数論の始祖とよばれている。フェルマーの業績の一部を述べてみると
(1)フェルマーの小定理 pを素数、aをpで割れない整数とすると
ap-1=1(modp)
が成り立つ。ここにa≡b(modp)はa-bがpで割り切れることを意味する記号で、ガウスにより導入されたものである。
(2)p≡1(mod4)なる素数pは二つの平方数の和として表せる。
(3)ペル方程式x2-Ay2=1の研究。
などである。フェルマーは証明をほとんど残さなかったが、その言明した命題の大半は現在証明が得られている。ディオファントスの『数論』のピタゴラス数に関する記述から思い付いたという、フェルマーの予想とよばれた命題は、長くその真偽がわからなかったが、フェルマーがこの問題を提起してから約360年後の1994年、プリンストン大学教授のワイルズAndrew Wiles(1953― )によって問題の証明が完成され、1995年にその証明が正しいことが確認された。その命題を現在の記法で述べると、nが3以上の自然数であるとき
xn+yn=zn
を満たす自然数x、y、zは存在しない、というものである。
フェルマーに続く時代の整数論にもっとも大きな貢献をした数学者はオイラーである。オイラーは、nが3の場合にフェルマーの定理が正しいことを証明した。またフェルマーの言明した前記の4n+1の形をした素数が平方和に表せるという命題も、オイラーが証明を与えた。
[足立恒雄]
近代の整数論
近代の整数論はガウスによって基礎づけられた。1801年刊行の『数論講究』Disquisitiones Arithmeticaeからいくつかの結果を拾ってみると
(1)作図可能な正多角形の確定。
(2)自然数の素因数分解とその一意性の厳密な証明。
(3)ガウスの整数の導入とその基本的性質の研究 x+iy(x、yは整数)の形の複素数をガウスの整数という。ガウスの整数の整除を定義し、素因数分解の一意性を証明した。これは後の代数的整数論の出発点となった。
(4)平方剰余の相互律 a、bを互いに素な整数とするとき、aが法bの平方剰余であるとは、a≡x2(modb)を満たす整数xが存在するときである。このとき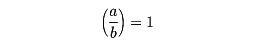
と表す。そうでないとき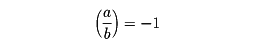
と表し、aは法bの平方非剰余であるという。ガウスは次の3法則を証明した。ここにp、qは相異なる奇素数とする。
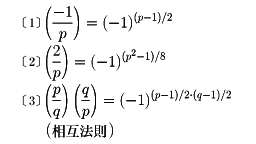
〔3〕の相互法則は整数論におけるきわめて重要な定理である。
(5)二元二次形式の研究の完成
ax2+bxy+cy2=d (a, b, c, dは整数)
の形の不定方程式について最終的、徹底的な研究がなされている。
ディリクレはガウスの『数論講究』を常時携帯し研究したといわれる。ディリクレの整数論上のおもな業績は解析的手法の導入である。たとえば、初項と公差が互いに素な等差数列中には素数となる項が無数にあることを主張する定理(算術級数定理)は彼によって証明された。その後、解析的整数論は発展を遂げて、1896年にはアダマールとド・ラ・バレ・プーサンCh. de la Vallée-Poussinによりガウスの予想した素数定理が複素関数論の深い結果を用いて証明された。
ガウスに始まる複素整数論はクンマーによるフェルマーの予想の研究によって飛躍を遂げ、現今の代数的整数論へと発展した。素因数分解の一意性が成り立たない場合があることを明確に意識していたクンマーは、円分体において理想数という概念を導入して一意性の回復をした。現今の用語では因子論とよばれる概念である理想数は、デーデキントによってイデアルという実体を与えられた。イデアルは集合論が意識的な形で数学に使用された最初ではないかと思われる。イデアル論とガロアの理論が結合して活躍の場を与えられた形の代数的整数論はヒルベルトによって整理され、高木貞治(たかぎていじ)の類体論へと道が開かれたのである。整数論はいままで述べたように代数的整数論、解析的整数論のほかに、幾何学的手法を用いる研究、不定方程式論固有の研究、また1960年代以降話題になりつつある数学基礎論による研究などがある。
不定方程式論におけるもっとも輝かしい成果の一つであるジーゲルの有限性定理を述べておく。f(x, y)を整数係数の多項式とし、
f(x, y)=0……〔1〕
から定まる曲線が二次曲線とは本質的に違っているものとする。厳密にいえば種数が正であるとする。このとき〔1〕は整数解を有限個しかもたない。この定理をジーゲルCarl Ludwig Siegel(1896―1981)は1929年に証明することに成功した。〔1〕の解の大きさをf(x)の係数から評価することは一般的にはまだ解決されていない問題であるが、ベーカーAlan Bakerは
y2=x3+ax+b
という形を含むいくつかの場合に解の限界を与えることに成功している。
一方、ヒルベルトは、不定方程式が解を有するかどうかを判定する一般的なアルゴリズムを求めよという問題(ヒルベルトの第10問題)を提起したが、マチャセビチYuri Matijasevicによれば、そういうアルゴリズムは存在しない(証明1970年)。これには帰納的関数の考えをはじめとする基礎論的手法が用いられており、数学界に大きな衝撃を与えた。この分野も一定の発展が期待されるであろう。
[足立恒雄]
百科事典マイペディア 「整数論」の意味・わかりやすい解説
整数論【せいすうろん】
→関連項目弥永昌吉|完全数|算術|リーマン
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「整数論」の意味・わかりやすい解説
整数論
せいすうろん
theory of numbers
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

