関連語
精選版 日本国語大辞典 「原始関数」の意味・読み・例文・類語
げんし‐かんすう‥クヮンスウ【原始関数】
- 〘 名詞 〙 その導関数が、あたえられた関数 f(x) に等しくなるような関数の、f(x) に対する称。基関数。
ブリタニカ国際大百科事典 小項目事典 「原始関数」の意味・わかりやすい解説
原始関数
げんしかんすう
primitive function
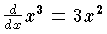 において,x3 は 3x2 の原始関数である。任意の関数 f(x) に対しては,必ずしも原始関数が存在するとはかぎらないが,連続関数ならば,その原始関数が存在する。 F(x) が f(x) の1つの原始関数ならば,他の原始関数はすべて F(x)+C ( C は任意の定数) で与えられる。一般に f(x) の原始関数を一括して,記号 ∫f(x)dx で表わす。連続関数については,原始関数は不定積分と一致する (微分積分学の基本定理) ので,原始関数という用語を使わず,不定積分あるいは単に積分と呼ぶことが多いが,理論上両者は別の概念である。
において,x3 は 3x2 の原始関数である。任意の関数 f(x) に対しては,必ずしも原始関数が存在するとはかぎらないが,連続関数ならば,その原始関数が存在する。 F(x) が f(x) の1つの原始関数ならば,他の原始関数はすべて F(x)+C ( C は任意の定数) で与えられる。一般に f(x) の原始関数を一括して,記号 ∫f(x)dx で表わす。連続関数については,原始関数は不定積分と一致する (微分積分学の基本定理) ので,原始関数という用語を使わず,不定積分あるいは単に積分と呼ぶことが多いが,理論上両者は別の概念である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
改訂新版 世界大百科事典 「原始関数」の意味・わかりやすい解説
原始関数 (げんしかんすう)
primitive function
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「原始関数」の意味・わかりやすい解説
原始関数【げんしかんすう】
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の原始関数の言及
【積分】より
…このように,与えられた区間で連続な任意の関数fに対して,それを導関数とする関数Fが存在する。この関数Fをもとの関数fの原始関数という。このときFに定数を加えても同じfの原始関数であるが,逆にfの任意の原始関数Gに対して(G-F)′=f-f=0となるから,G-Fはある定数Cに等しい。…
※「原始関数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

