シェーンフリースの記号（読み）シェーンフリースのきごう

最新 地学事典

シェーンフリースのきごう
シェーンフリースの記号

Schoenflies notatlon

晶族（点群），空間群を表す記号の一種。ただし，国際記法はヘルマン─モーガンの記号がより一般的。空間群の表記では，その空間群の属する晶族の記号の右肩に番号を付して表す。例えば…等。各晶族における空間群の順序は シェーンフリースが空間群を導出したときに付した順序を踏襲。

執筆者：丸茂 文幸・大藤 弘明

参照項目：ヘルマン─モーガンの記号

出典　平凡社「最新 地学事典」

化学辞典 第2版

シェーンフリースの記号
シェーンフリースノキゴウ
Schönflies symbol, Schönflies notation

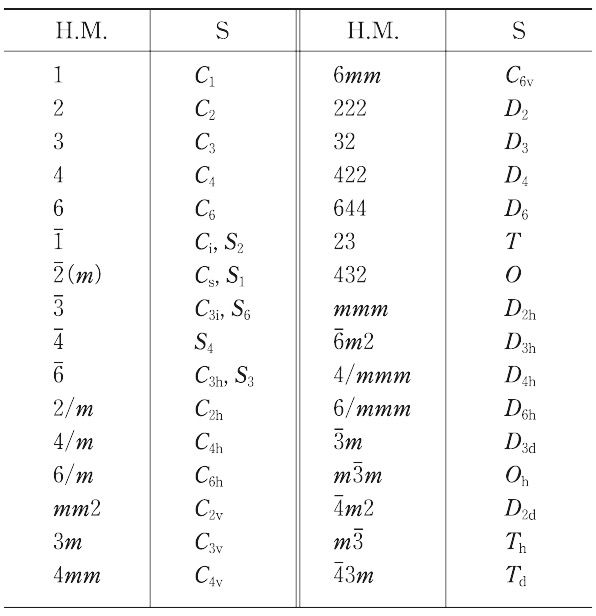
点群または晶族，もしくは空間群の記号の一つ．とくに点群の記号としては直感的で便利なものでいまでもよく用いられている．結晶の晶族の場合は次のように決める．1本のn回回転軸のみを含む場合は C_n と書く(n ＝ 1，2，3，4，6)．対称心のみの場合は C_i，鏡映面のみの場合は C_s，4回回映軸のみの場合は S₄ と書く．C_n に直交した2回回転軸を加えたものを D_n(n ＝ 2，3，4，6)，C_n に垂直な鏡面をもつものを C_nh(n ＝ 2，3，4，6)，C_n と回転軸を含む鏡面をもつものを C_nv(n ＝ 2，3，4，6)，D_n にさらにn回回転軸と直交する鏡面が加わったものを D_nh(n ＝ 2，3，4，6)，D_n に対しさらにn回回転軸を含み，かつそれに垂直に2本の2回回転軸の方向を二分する鏡面を加えたものを D_nd(n ＝ 2，3のみ)，C₃ に対称心を加えたものを C_3i とする．以上のほか，1本の3回回転軸で関係づけられる3本の直交した等価な2回回転軸を含むものをT，Tに2回回転軸と直交する鏡面を加えたものを T_h，Tの2回回転軸を4回回転軸で置き換えたものをO，Oの4回回転軸のかわりに4回回反軸を置き，それに対してさらに1本の4回回反軸を含み，ほかの2本の4回回反軸と45°の角で交わる鏡面を加えたものを O_h と書く．以上の32種類が晶族のすべてであって，点群もこれに対応している．空間群の場合は，空間群の一つ一つがどれかの点群から導かれるので，関係した点群の記号の右肩に，シェーンフリースの導いた順に従って番号1，2，3，…をつけたものを記号とする．たとえば，点群 C_2h に対し空間群は C_2h¹ から C_2h⁶ まで，D_2h に対しては D_2h²⁸ までの空間群が存在する．このように，この記号では各空間群に対応する対称要素の配列の様子がわからないので，空間群の記号としてはあまり用いられていない．なお，結晶以外の点群の場合の記号もだいたい結晶の場合に準じて決められる．[別用語参照]ヘルマン-モーガンの記号

出典　森北出版「化学辞典（第2版）」