化学辞典 第2版 「点群」の解説
点群
テングン
point group
並進操作を伴わない結晶や分子がまったく同じに見える対称操作の集合がつくる群のこと.分子や結晶の形の対称性を記述するのに広く用いられる.結晶においては,対称操作をするための独立な対称要素は,1,2,3,4,6回の回転軸,反転中心(対称心),鏡映面(対称面)および4回回映軸(回反軸)の8種類である.これらの組合せは32通りの群になる.点群は数学的表現であり結晶形態の分類による32の晶族と対応する(図参照).等軸晶系5,正方晶系,六方晶系各7,三方晶系5,斜方晶系,単斜晶系各3,三斜晶系2である.点群の表記はヘルマン-モーガンの記号(図中( )内の表記)あるいは分子の対称を表すシェーンフリースの記号で表す.ある結晶あるいは分子がどの点群に属するかを決めるには,その分子の対称要素と比較する.おもな対称要素と対称操作,その記号を表1に示す.またよく現れる点群と対称要素,分子の形の例を表2にまとめる.点群は結晶や分子の対称性,結晶性,物理的性質の予測と記述に有用である.さらに正確な結晶構造の対称性を考慮するときには並進操作を加えた230種の空間群に拡張される.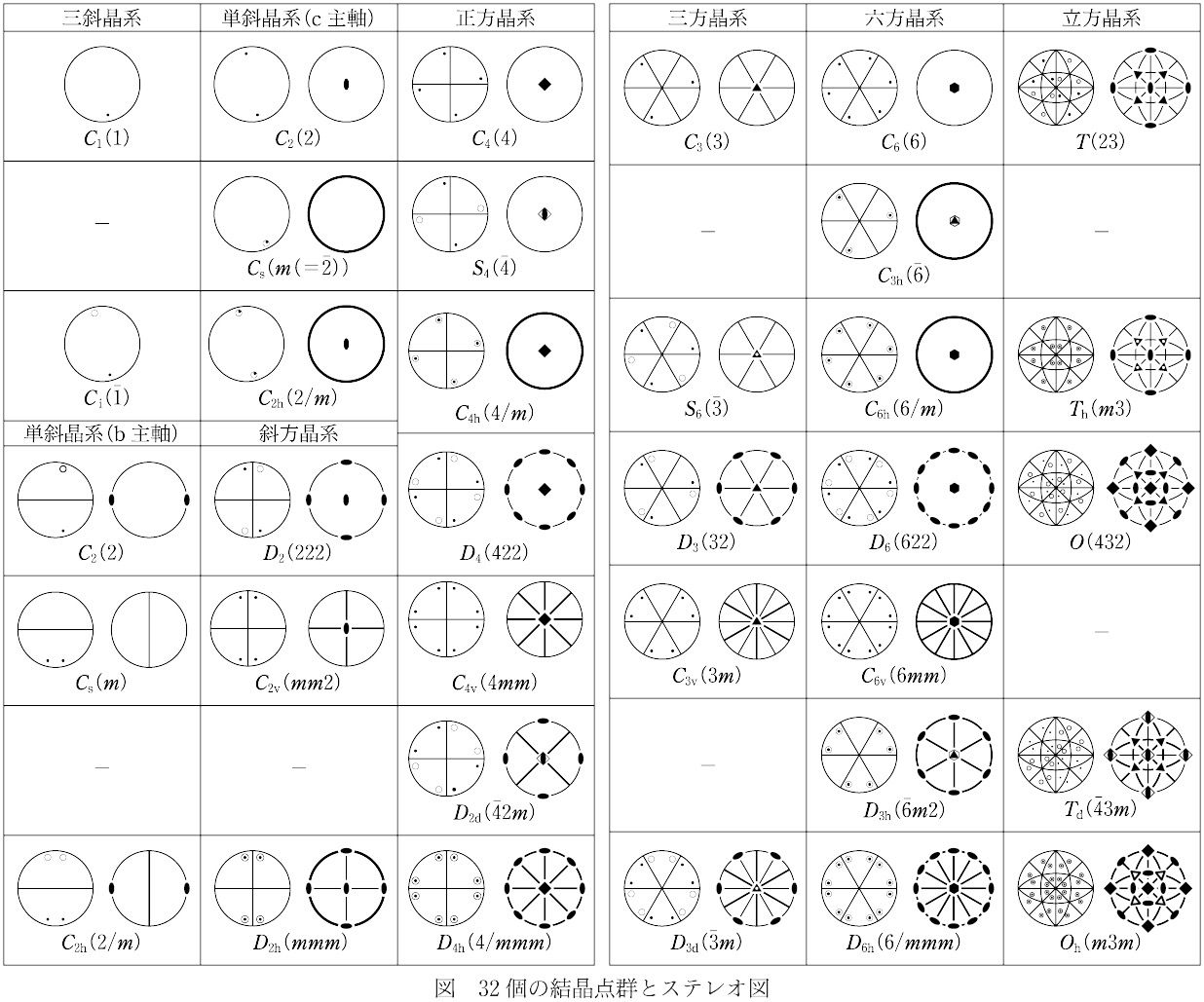

出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
日本大百科全書(ニッポニカ) 「点群」の意味・わかりやすい解説
点群
てんぐん
point group
結晶に可能な8種の対称要素、すなわち1、2、3、4、6回回転軸(本義回転軸)および1、2、4回回反軸(転義回転軸)の可能な組合せで得られる32種の有限な群。これらは32種の晶族に対応しており、結晶族群ともよばれる。個々の点群には、ヘルマン‐モーガンの記号Hermann-Mauguin's notationあるいはシェーンフリースの記号Schoenflies' notationが与えられるが、結晶構造の記載には一般に前者を用いる。後者は分子構造の対称を示すのに用いられることが多い。
独立した分子の構造には、結晶構造では許されない対称要素、たとえば5回軸や7回軸の存在も可能であり、分子の中心点における対称の群表示も行われるが、分子の場合には点群とはいわず、分子群molecular groupという。
[岩本振武 2015年8月19日]
『H・H・ヤッフェ、M・オーチン著、齊藤喜彦訳『現代化学シリーズ31 群論入門――化学における対称性』(1966・東京化学同人)』▽『中崎昌雄著『化学と対称性――群論入門』(1976・南江堂)』
百科事典マイペディア 「点群」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
最新 地学事典 「点群」の解説
てんぐん
点群
point group
結晶における対称の要素の組合せを点の座標によって幾何学的に記述したもの。32通りあり,晶族と一致する。
執筆者:高野 幸雄
参照項目:晶族
出典 平凡社「最新 地学事典」最新 地学事典について 情報
世界大百科事典(旧版)内の点群の言及
【結晶】より
…また,結晶面として現れるある格子面と対称的に同価な他の格子面もやはり結晶面として形態に現れることも経験的に知られている。
[点群,結晶族]
微視的なn回らせんや映進の並進成分tは巨視的には見ることができないから,それらは巨視的にはそれぞれn回回転と鏡映とに等しくなり,また微視的な格子並進も巨視的には均質な連続体となるから,その結晶の任意の点Oを原点にとって,すべての対称要素がOを通るとみなしてよいことになる。互いに平行に繰り返して存在する結晶構造の微視的な対称要素と,それらと方向を同じくして原点Oを通る巨視的な対称要素との対応を矢印で示せば,n回回転およびらせん軸→n回回転軸,n回回反軸(n>2)→n回回反軸,鏡映面および映進面→鏡映面,対称心→対称心となる。…
※「点群」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...