ヘルマン-モーガンの記号（読み）ヘルマン－モーガンのきごう

最新 地学事典

ヘルマン－モーガンのきごう
ヘルマン-モーガンの記号

Hermann-Mauguin symbols

結晶の属する点群あるいは空間群を表す記号法の一種。ブラベ格子をP, F, I，A，B，C，H，Rとしてそれぞれ単純，面心，体心，a・b・c面心，六方，菱面体格子を表現する。回転軸は次数1, 2, 3, 4, 6, 回反軸は, , ……，鏡面をmなど対称の操作を記号で表す。現在では最も広く用いられている点群・空間群の表現法で『International Tables for X- ray Crystallography』に採用されている。

執筆者：河原 昭

参照項目：ステレオ投影と対称操作・32晶族

出典　平凡社「最新 地学事典」

化学辞典 第2版

ヘルマン-モーガンの記号
ヘルマンモーガンノキゴウ
Hermann-Mauguin's symbol, Hermann-Mauguin notation

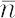点群または晶族，もしくは空間群の記号の一つ．シェーンフリースの記号に比べてとくに空間群の表記上すぐれているので，今日ではほとんどこれが利用されている．点群の場合は，一般にn回回転軸の操作をn(n ＝ 1，2，3，4，6)，n回回反軸の操作を(n ＝ 1，3，4，6，ただしn ＝ 2のみ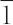鏡映を意味するmを書く)とし，点群を記載するのに必要かつ十分な独立な対称の要素を重要度の順に並べてつくる．n回回転軸に垂直な鏡面があるときは，n/mと書く．そこに記載された対称要素から当然存在が帰結されるその他の対称要素は一般に省略される．32種類の点群の簡略形は次のとおりである((　)内は同じ点群に対するシェーンフリースの記号)．1(C₁)，(C_i)，2(C₂)，m(C₂)，2/m(C_2h)，222(D₂)，mm2(C_2v)，mmm(D_2h)，4(C₄)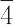，(S₄)，4/m(C_4h)，422(D₄)，4mm(C_4v)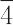，m2(D_2d)，4/mmm(D_4h)，3(C₃)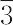，(C_3i)，32(D₃)，3m(C_3v)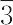，m(D_3d)，6(C₆)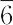，(C_3h)，6/m(C_6h)，622(D₆)，6mm(C_6v)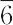，m2(D_3h)，6/mmm(C_6h)，23(T)，m3(T_h)，432(O)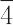，3m(O_d)，m3m(O_h)．空間群の場合は，最初に空間格子の型をP(りょう面体以外の単純格子)，I(体心)，F(面心)，A，B，C(以上底心)，R(りょう面体)で示し，次に点群の記号に対応する対称要素を点群記号の順に並べる．このとき，回転軸，回反軸，および鏡面は点群の場合と同じ記号を用い，らせん軸と映進面の場合はそれぞれの記号をもって点群記号の相当する場所を置き換える．たとえば，P 2₁/cは単純格子で，主軸が 2₁ となるらせん軸であり，それに直交するc軸方向の映進軸があることを表し，関係点群は2/mである．ただし，空間群によっては記号法に多少の例外があり，また，いくつかの異なる表現もある．

出典　森北出版「化学辞典（第2版）」