トマス‐フェルミモデル（その他表記）Thomas-Fermi model

法則の辞典

トマス‐フェルミモデル【Thomas-Fermi model】

原子内の多電子系の量子力学の近似的解法としてトマス（L. H. Thomas）とフェルミ（E. Fermi）の二人によって独立に提案されたものである．

おのおのの電子は原子番号 Z の原子核や他の電子のつくる平均的な静電ポテンシャル V（r）の中を動いていると考える．r は位置のベクトルである．電子の分布している空間を小さな体積 dv となるような細胞に分割し，この細胞の中では静電ポテンシャルは一定で，その一辺の長さは電子のド＝ブロイ波長よりも十分大きいと仮定する．この仮定では，細胞内の電子は自由電子気体と考えてもかまわない．電子はフェルミ‐ディラック統計＊に従うので，電子の数密度を n（r） とするならば，細胞内に含まれる電子の運動エネルギーの総和は，電子の電荷（単位電荷）を ε_k とし，ボーア半径を a₀ とすると

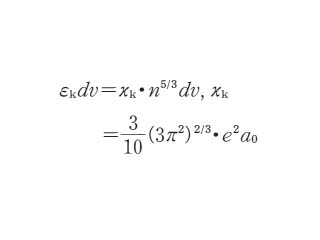
のように書ける．この近似を「トマス‐フェルミ近似」という．この近似のもとで電子の全エネルギーを求めると，

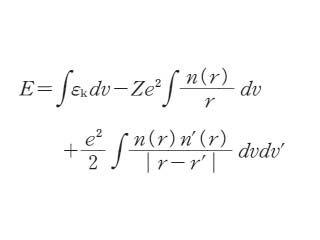
となる．第二項は原子核と電子の間のクーロンエネルギー項，第三項は電子間のクーロンエネルギー項に当たる．これに電子の総数 N が一定（＝∫ n（r）dv）であるという条件を入れて，上の式が極小となる条件を求めることになる．ポテンシャル V（r） と電子密度 n（r） の間にはポアッソンの方程式が成立するはずだから，計算を簡便にするためにいくつかのパラメータを導入すると，トマス‐フェルミの方程式＊が得られる．

出典　朝倉書店