共同通信ニュース用語解説 「量子力学」の解説
量子力学
電子や光の粒(光子)などの極めて小さな物質の挙動を説明する理論。量子力学の世界では、身近な現象から定式化された古典的な物理学では説明がつかない不思議な現象が起きることがあり、量子もつれもその一つ。光子などの量子がどんなに離れていても互いの状態が常に関連するという現象で、世界各国で開発が進む量子コンピューターや情報の盗み見を防ぐ次世代技術「量子暗号」の核となっている。
更新日:
出典 共同通信社 共同通信ニュース用語解説共同通信ニュース用語解説について 情報
精選版 日本国語大辞典 「量子力学」の意味・読み・例文・類語
りょうし‐りきがくリャウシ‥【量子力学】
- 〘 名詞 〙 素粒子・原子・原子核・分子など微視的な粒子に関する、古典力学とは異なる力学体系。一九二五~二六年頃から、ハイゼンベルクの行列力学、シュレーディンガーの波動力学、ディラックの変換理論などにより統一的体系が築かれた。
- [初出の実例]「量子力学にしても、波動力学にしても」(出典:量的と質的と統計的と(1931)〈寺田寅彦〉)
改訂新版 世界大百科事典 「量子力学」の意味・わかりやすい解説
量子力学 (りょうしりきがく)
quantum mechanics
電子や陽子,中性子などの素粒子,さらにそれらより小さい基本粒子のレベルで諸現象を統制する理論体系。このレベルの世界では粒子と波動の二重性が顕著であり,たとえば水素原子において原子核である陽子のまわりを回る電子は,エネルギーの確定した運動をするとき,一定の軌道を刻々に速度を変えながらたどっていくのではない。こうした粒子としての描像に代えてこの場合の電子は原子核のまわりに広がって振動する波動として表現される。だからといって電子が分解して空間に拡散してしまったわけではなく,電子の位置を観測すれば電子は(かけらではなく,まるまる)1点に見いだされることになり,ここに粒子性が現れるのである。また光は,波動のようにふるまって回折したり干渉したりもするが,たとえば電子に衝突する場合には一定のエネルギーと運動量をもったかたまり(光子,フォトン)の姿で現れる。原子が光をだす場合にも,光はじわじわとにじみ出るのではなくエネルギーのかたまりとして瞬間的に出るのである。このように,電子や光子,陽子,中性子などはかりに粒子的な名で呼ばれてはいるが,〈ときに波動の姿で現れ,ときに粒子の姿で立ち現れるあるもの〉とでもいうほかない。量子力学は,粒子と波動のことばをつかいながら,その両側面に統一的な記述をあたえる。統一のための橋渡しをするのが量子力学の確率解釈である。
波動と確率
量子力学的な粒子(たとえば原子の中の電子)の運動は波動で表現することができる。波動というものは,水面におこる波のようすから想像されるように,空間に広がり刻々に形を変えていくのが一般である。量子力学的な粒子について,その運動を表す波動の一時刻tにおける形--その瞬間にシャッターを押して撮った写真--を,その粒子の時刻tにおける〈状態〉とよぶ。粒子の状態とは,古典力学だったら,その時刻tにおける粒子の位置と速度のことである。この二つが知れると以後の時刻におこることがニュートンの運動方程式から完全に決まるからである。同様に,量子力学においても,運動を表現する波動に対して,一時刻tにおけるその形から以後の移りゆきを完全に決める方程式があり,それを提出した人の名をとってシュレーディンガーの波動方程式とよばれる。空間の各点における波動の値(複素数)をあたえる関数は波動関数とよばれる。波動方程式は波動関数に対する偏微分方程式である。量子力学的な粒子の運動が波動で表されるといっても,粒子が粉々になって空間に拡散するわけではない。前にも述べたとおり,一時刻tに粒子の位置を観測する実験をすれば1点に確定した結果が得られる。ただ,それがどこになるかは,その時刻の状態(その時刻tにおける波動関数ψt)が知れていても観測より前に予言することはできない。予言できるのは,〈ここに粒子が見いだされる確率はこれだけ,あそこに見いだされる確率はこれだけ,……〉ということのみであって,一般に空間の位置rに見いだされる確率はその点における波動関数の値ψt(r)の2乗であたえられる。正確にいえば,点rの近傍の微小体積dvに粒子の見いだされる確率は|ψt(r)|2に体積dvをかけて得られるので,|ψt(r)|2自身は粒子の存在確率密度とよばれている。ただし,|ψt(r)|2dvを全空間にわたって寄せ集めた値は1になるようにしておくのである。必要ならψtの大きさを全空間で一定の倍率で縮小または拡大するわけで,これを規格化という。時刻tに観測が行われ,粒子が位置r=aに見いだされた上は,もう一度その直後に粒子の位置を観測するとr=aとほとんど違わない結果になる。これは初めの観測で,波動関数がr=a以外の場所では0であるような形に変えられたことを意味する。観測による波動関数のこの変化を点aへの波束の収縮とよぶ。それ以後,波動関数は点aからシュレーディンガーの波動方程式に従って広がっていくことになる。
定常状態
シュレーディンガー方程式の解のなかには,波動が空間のあらゆる点でいっせいに足並みそろえて振動するようなものがある。これは,2点の間にピーンと張った弦の振動の場合なら固有振動に相当するもので,量子力学の波動の場合にもその振動数は特定の一連の値(固有振動数)ν0,ν1,……に限られる。こうしたψの固有振動は,それぞれ量子力学的粒子のエネルギー確定の運動を表し,それをしている粒子は定常状態にあるといわれる。定常状態のエネルギーはそれぞれの振動数にプランク定数hをかけたhν0,hν1,……であたえられ,系のエネルギー準位とよばれる。たとえば水素原子の電子のエネルギー準位は-13.6eV/n2と書ける(n=1,2,……)。量子力学的な系のエネルギーのとりうる値はその系のエネルギー準位の値E0=hν0,E1=hν1,……に限られ,多くの場合とびとびになる。原子をはじめ量子力学的な系のだす光が多くの場合に線スペクトルをなすのはそのためである。実際,系がエネルギーEnの定常状態からより低いEn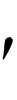 の定常状態に遷移するときにでる光の振動数
の定常状態に遷移するときにでる光の振動数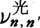 は,エネルギー保存則から
は,エネルギー保存則から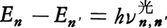 で決まり,nとn′に応じたとびとびの値になる。このとき定常状態で固有振動する波動関数をψnと書けば,系が光をだす場合,その波動ψがある時刻に急にψnから別のψn
で決まり,nとn′に応じたとびとびの値になる。このとき定常状態で固有振動する波動関数をψnと書けば,系が光をだす場合,その波動ψがある時刻に急にψnから別のψn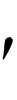 に変わるのではなく,ψは両者の重ね合せαnψn+αn
に変わるのではなく,ψは両者の重ね合せαnψn+αn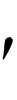 ψn
ψn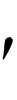 で時間の経過につれてαnが小さくなりαn
で時間の経過につれてαnが小さくなりαn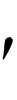 が大きくなっていく。こうした変化は考える系と放射の場との相互作用を考慮に入れて初めておこることで,全系に対するシュレーディンガー方程式で決められる。そして考える系が時刻tにまだ光をださず最初の状態にとどまっている確率が|αn|2であたえられ,すでに光をだして下の状態に遷移している確率は|αn
が大きくなっていく。こうした変化は考える系と放射の場との相互作用を考慮に入れて初めておこることで,全系に対するシュレーディンガー方程式で決められる。そして考える系が時刻tにまだ光をださず最初の状態にとどまっている確率が|αn|2であたえられ,すでに光をだして下の状態に遷移している確率は|αn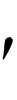 |2であたえられる。こうして量子力学は光の放出という瞬間的な遷移(時間的に不連続な過程)を確率を介して波動関数αnψn+αn
|2であたえられる。こうして量子力学は光の放出という瞬間的な遷移(時間的に不連続な過程)を確率を介して波動関数αnψn+αn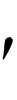 ψn
ψn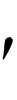 の時間空間的に連続な変化に直して記述している。
の時間空間的に連続な変化に直して記述している。
観測量と固有関数
シュレーディンガー方程式は一般に,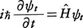 という形をしている(i2=-1,ħ=h/2π)。Ĥは,たとえば水素原子の電子の場合でいえば,電子の質量をm,電荷を-e,真空の誘電率をε0として,
という形をしている(i2=-1,ħ=h/2π)。Ĥは,たとえば水素原子の電子の場合でいえば,電子の質量をm,電荷を-e,真空の誘電率をε0として,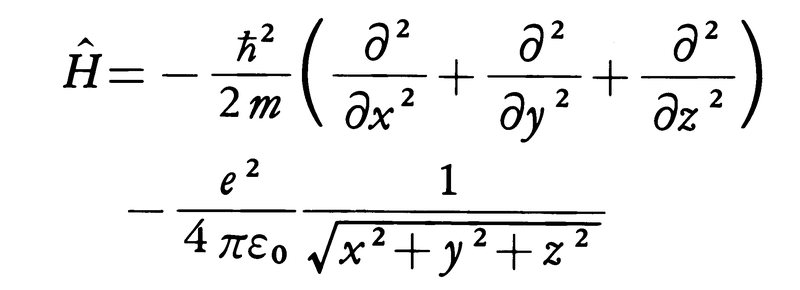
の形であり,電子の位置座標に相当するr=(x,y,z)の関数ψt=ψt(x,y,z)に作用してこれを別の関数に変える働きをもつ。この種の働きをもつものを一般に演算子とよぶ。そのもっとも単純なものは関数をxで微分する微分演算子∂/∂xである。また上のĤの中に見える,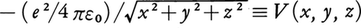 は関数ψt(x,y,z)をV(x,y,z)ψt(x,y,z)に変える掛算演算子である。シュレーディンガー方程式に現れるĤはハミルトニアン演算子とよばれるが,上の例では2階の微分演算子と掛算演算子の和になっており,一般に波動関数ψtを複雑なしかたで変えることが想像されよう。シュレーディンガー方程式の解のうちでとくに定常状態にあたるものは,
は関数ψt(x,y,z)をV(x,y,z)ψt(x,y,z)に変える掛算演算子である。シュレーディンガー方程式に現れるĤはハミルトニアン演算子とよばれるが,上の例では2階の微分演算子と掛算演算子の和になっており,一般に波動関数ψtを複雑なしかたで変えることが想像されよう。シュレーディンガー方程式の解のうちでとくに定常状態にあたるものは,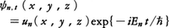 という固有振動に特有の形をしており,unは,
という固有振動に特有の形をしており,unは,
Ĥun=Enun
をみたす。つまりunは,Ĥを作用させてもEn倍される以外に関数形が変わらないという特別の性質をもっている。どんな関数がこの性質をもつかは演算子Ĥによって違うが,非常に限られた種類のものであることは確かなので,それらを一括して演算子Ĥの固有関数とよぶ。そしてĤを作用させたときの倍率Enを固有値とよぶ。前項に述べたことと併せていえば,量子力学的な系のエネルギーがとりうる値は,この系のハミルトニアン演算子Ĥの固有値に限られる。その系が時刻tに状態ψtにあるときエネルギーの観測をするものとすれば,観測前に予言できることは,観測値はĤの固有値E0,E1,……,En,……のどれかに限られ,このうちのEnが得られる確率は|γn|2だということまでである。ただしγnはψtを,
ψt=γ0u0+γ1u1+……+γnun+……
のようにĤの固有関数で展開したときの展開係数であって,前項のαnとは,
γn=αnexp{-iEnt/ħ}
の関係があり|γn|2=|αn|2である。
量子力学には,エネルギーに限らず他の力学量に関しても同様の構造がある。すなわち粒子の位置,運動量,運動エネルギー,……といった力学量のそれぞれに特有の演算子が対応し,それぞれの観測値と観測値ごとの確率は固有値と固有関数から上のようにして決められる。たとえば,粒子の位置座標には,
x^=x・, ŷ=y・, ẑ=z・
という掛算演算子が対応し(x・はxを掛けることを表す),運動量には,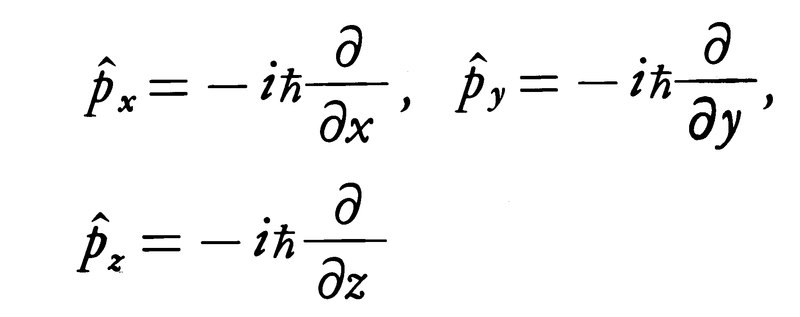
という微分演算子が対応する。さきに記したエネルギーの演算子Ĥが,古典力学のエネルギーの式,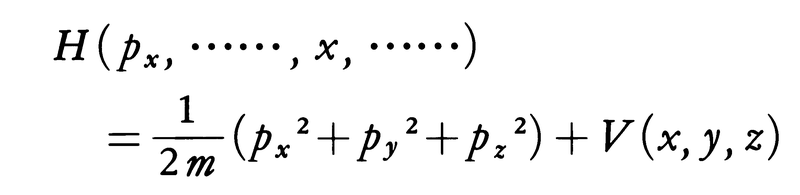
のpxをp^xで,……,xをx^で,……,おきかえれば得られることに注意しよう。つまり,量子力学において力学量に対応する演算子を構成するには,その力学量の古典力学的な表式をとって位置座標と運動量を対応する演算子でおきかえればよい。たとえば,粒子の角運動量Lの古典力学的な表式は,x成分でいえば,
Lx=ypz-zpx
であるから,量子力学でこれに対応する演算子は,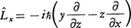 となる。ただし,この種の構成において座標と運動量の演算子の非可換性(次節で述べる)から問題がおこる場合があり,演算子の自己共役性を目標とする数学的考慮が必要となる。そのため,古典力学的なすべての力学量が量子力学のなかに対応する演算子をもつとは限らない。またスピンのように古典力学のなかに対応する量がないものもある。そこで,量子力学において自己共役な演算子をもつ物理量をとくに観測量(オブザーバブル)とよぶ。なお,物理量に対応すべき演算子に自己共役性を要求する物理的根拠は,この特性が次のことを保証し観測の確率解釈を可能にするところにある。(1)その演算子の固有値がすべて実数になる,(2)その演算子の固有関数が任意のψtを展開できるだけ十分にたくさんある(完全系をつくる)こと。
となる。ただし,この種の構成において座標と運動量の演算子の非可換性(次節で述べる)から問題がおこる場合があり,演算子の自己共役性を目標とする数学的考慮が必要となる。そのため,古典力学的なすべての力学量が量子力学のなかに対応する演算子をもつとは限らない。またスピンのように古典力学のなかに対応する量がないものもある。そこで,量子力学において自己共役な演算子をもつ物理量をとくに観測量(オブザーバブル)とよぶ。なお,物理量に対応すべき演算子に自己共役性を要求する物理的根拠は,この特性が次のことを保証し観測の確率解釈を可能にするところにある。(1)その演算子の固有値がすべて実数になる,(2)その演算子の固有関数が任意のψtを展開できるだけ十分にたくさんある(完全系をつくる)こと。
正準交換関係
一般に二つの演算子の積はその順序によって働きが違う。たとえば,位置座標と運動量の演算子の場合,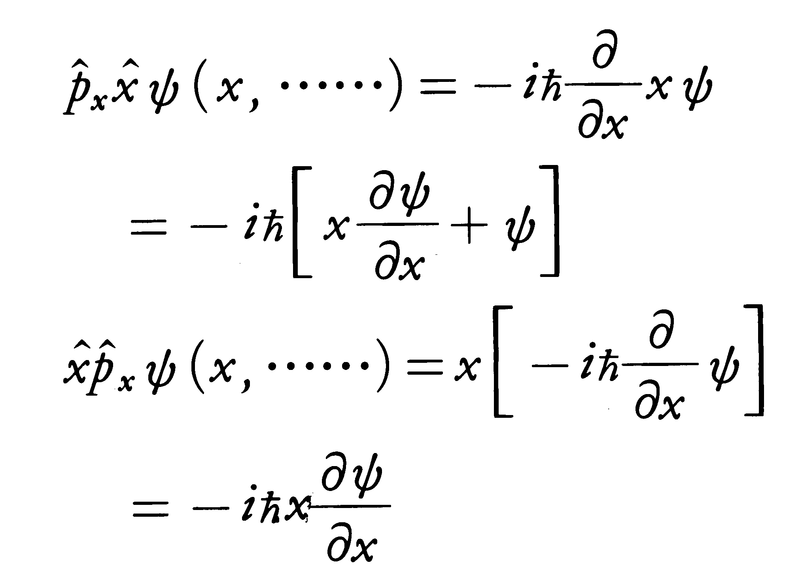
となり,演算の結果に,
(p^xx^-x^p^x)ψ=-iħψ
だけの差がでる。この式は,どんな関数ψに対してもつねに成り立つので,p^xx^-x^p^xという演算子が-iħを掛ける掛算演算子と同等なことを示している。一般にÂB^-B^Â≡[Â,B^]と書き,[Â,B^]が0ならÂとB^は可換,0でないなら非可換であるという。位置座標と運動量の他の成分についても計算すると,
[p^x,x^]=-iħ,[p^x,ŷ]=0,……,
[p^x,p^y]=0,[x^,ŷ]=0,……
となり,位置座標と運動量との同じ成分どうしは非可換,他の組合せはすべて可換であることがわかる。これを一括して正準交換関係とよぶ。実は,量子力学で位置座標と運動量に演算子を対応させるしかたは,先に記したもの以外にもいろいろある。この対応は正準交換関係をみたすものである限りどれを用いても実験と比較できる量の計算結果には差がでないことが証明される。これは正準交換関係が量子力学にとって真に基本的な要素であることを示している。
量子力学の歴史
ニュートンの力学とマクスウェルの電磁気学を柱とする古典物理学は,天体の運動と地上の諸現象を解き明かし,一時は,残る課題は諸定数の有効数字を増すことのみとさえいわれた。X線の発見(W.C.レントゲン,1895)とその波動性の確認(M.vonラウエ,1912)も,電子の粒子性の発見(J.J.トムソン,1897)も古典物理学によってなされたのだった。
古典物理学の限界
しかし,L.ボルツマンの気体分子運動論が予言した気体の比熱は実験値より大きく,分子が回転すべくして回転しないことを暗示していた。P.K.L.ドルーデの金属電子論(1900)は,一定温度の下で金属の電気伝導率と熱伝導率の比が金属の種類によらず一定になるというウィーデマン=フランツの法則を首尾よく説明したが,金属の比熱の計算値は実験とけた外れに違ってしまった。さらにラジウムの発見(キュリー夫妻,1898)はエネルギーの保存をはじめとして力学,熱力学を根底からゆるがした。放射能が原子の崩壊によることが明らかになった(ラザフォードとソディ,1902)後にも,シュワイドラーEgon Ritter von Schweidler(1873-1945)は単位時間当りの崩壊数に見られるゆらぎからこれがまったく偶然に支配されていることを読みとった(1905)。これは古典物理学の土台をなす因果律,決定論の破綻(はたん)を意味する。
量子の発見
古典物理学の限界をしるす作用量子hの発見(1900)は,しかし熱放射の研究から生まれた。溶鉱炉のような高温の炉をみたす光はどの波長で強くどの波長で弱いか。そのスペクトル分布が炉壁の温度のみにより材料によらないという普遍性をもつことは,熱力学により証明されていた(キルヒホフ,1860)。スペクトル分布の実測曲線は,気体分子運動論との類比から推測したウィーンの公式に短波長側でしかあわず,これを統計力学のエネルギー等分配の法則から批判し光と音波の類比に頼って導いたレーリーの公式には長波長側でしかあわなかった。M.プランクは両者を熱力学的考察により内挿し,一つの定数の値を調節すれば実測曲線に正確に一致するという公式(プランクの放射則)を得た(1900)。調節の結果,その定数は,
h=6.55×10⁻27erg・s
と決定された。この定数こそ今日プランク定数とよばれるものである(今日の値は6.58×10⁻27erg・s)。彼は新しい放射公式の含意をさぐって,緊張の1週間の後,電気をもった調和振動子が放射を吸ったり吐いたりしてこれと平衡し,振動子は温度Tの熱平衡状態にあるが,ただし振動数νの振動子のエネルギーはhνの整数倍に限られるというモデルをさがし当てた。振動子のエネルギーがhνの整数倍という不連続な値しかとらないことは,古典物理学からは理解しにくいなぞであったが,プランクは荷電粒子による光の放出の機構に未知の部分があり,それが明らかになればなぞも解けるだろうとする立場をとって,苦闘を続けた。
光量子
プランクの公式の革命的な含意をくみとったのはアインシュタインであった。1905年に彼は論文《光の発生と変換に関する一つの発見法的観点》を書き,振動数νの光はhνというエネルギーの粒子(光量子)の流れであるとして(光量子仮説),こう主張した。すなわち,これまで光はマクスウェルの方程式に従う電磁場の波動であるとされてきたが,光学的観測では〈瞬間的な値ではなしに時間的平均値が問題にされてきた〉にすぎず,波動像が回折,反射,屈折,分散の現象で完全に証明されているとしても〈光の発生や変換に適用したら実験に矛盾することもありうる〉。アインシュタインは,光の変換の例として光ルミネセンスと光電効果をあげ,前者に対するストークスの法則と後者に対するレーナルトの法則が光量子の観点から直截的に理解されることを示した。しかし,光電効果において金属板から飛び出してくる電子のエネルギーの最大値をhν-Pとしたアインシュタインの公式(Pは電子が金属から脱出するのに使うエネルギー)が実証されたのは16年であり,R.A.ミリカンによる。また光が実際にエネルギーと運動量のかたまりとして電子と衝突することがコンプトン効果により実証されるのは23年になってからである。
粒子と波動の二重性
光量子はエネルギーの表式hνに振動数を含み,波動ぬきでは語れない。アインシュタインは,プランクの放射式を用いて空洞内の小体積のエネルギーのゆらぎを計算し,粒子の出入りで解釈される項と波動の干渉で解釈される項の和になることを示した(1909)。同じ年にG.I.テーラーは,干渉計の中に同時には2個以上の光量子が存在しないくらい微弱な光でも長い時間かければ干渉縞をつくることを実証した。これは干渉を多数の光量子の相関によると見るアインシュタインの観点を否定するものであった。
力学現象の量子化
電磁場が量子性を示すなら力学現象も示すはずだという考えから,アインシュタインは1907年に,固体をつくっている分子の調和振動もhνおきの離散的エネルギー値のみとりうるとして固体の比熱を計算した(アインシュタインの比熱式)。固体の比熱は気体定数をRとして高温では1mol当り3Rだが(デュロン=プティの法則),温度を下げると減少し絶対零度で0になるという彼の結論は,彼の入手できたダイヤモンドなどの測定結果とよく一致した。この理論には,熱力学の第3法則を発見して低温の熱現象の実験を精力的に進めていたH.W.ネルンストが注目し,比熱の実測により強く支持したので,エネルギー量子のアイデアが広く受け入れられるようになった。
量子化の規則の探究
人々の関心は調和振動子に限らず一般の系の運動を量子的にする規則の探究にむかった。1911年にプランクは1自由度力学系が位相空間に描く軌跡の囲む面積をhの整数倍とし,13年にP.J.W.デバイも同調した。この年にP.エーレンフェストは単位時間当りの回転数がνの二次元回転子のエネルギーを,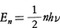 として量子化し(因子1/2はこの系が位置エネルギーを欠くのでつけた),
として量子化し(因子1/2はこの系が位置エネルギーを欠くのでつけた), を得た(Iは回転子の慣性モーメント)。これによって水素ガスの比熱が低温で分子の回転なしの値になること(A.T.オイケン,1912)を説明したのである。16年にはプランクとP.シェラーが同様にして並進運動を量子化した。
を得た(Iは回転子の慣性モーメント)。これによって水素ガスの比熱が低温で分子の回転なしの値になること(A.T.オイケン,1912)を説明したのである。16年にはプランクとP.シェラーが同様にして並進運動を量子化した。
原子の構造
原子の力学的モデルをつくる試みは早くからあったが(長岡半太郎の土星模型,J.J.トムソンの陽球模型),実験的基礎を得たのはE.ラザフォードによる原子核の発見(1911),N.ボーアによる原子内電子数の決定(1913)のときである。ボーアは質量と電気素量だけでは原子の大きさを導くのに不足であることを次元解析から知り,原子構造論におけるプランク定数の役割を見抜いた。またマクスウェルの電磁気学によれば,原子核のまわりを公転する電子は,その加速度のゆえに放射をだしエネルギーを失って瞬時に核に墜落することから,電磁気学の原子内への適用をやめた。彼は,原子内の電子に対し次の仮定をおく。(1)電子は定常状態とよぶ特別の運動のみをし,その状態では加速度があるにもかかわらず放射をしない。(2)電子はエネルギーEnの定常状態から,より低いEn のそれに遷移することがあり,そのとき,
のそれに遷移することがあり,そのとき, で決まる振動数νの光を放出する。(3)電子の運動はニュートンの運動方程式に従うが,しかし初期条件に応じて運動はさまざまになるという古典力学の特徴は失われ,量子条件をみたす運動だけが定常状態として実現する。
で決まる振動数νの光を放出する。(3)電子の運動はニュートンの運動方程式に従うが,しかし初期条件に応じて運動はさまざまになるという古典力学の特徴は失われ,量子条件をみたす運動だけが定常状態として実現する。
ボーアは,電子が核を中心として円運動するものとして,運動方程式から単位時間当りの公転数νとエネルギーEの間に,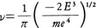 の関係があることを導き,定常状態のE=En,ν=νnは量子条件,
の関係があることを導き,定常状態のE=En,ν=νnは量子条件,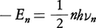 で選ばれるものとして,
で選ばれるものとして,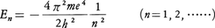 を得た。そして,振動数条件から得られる光の振動数,
を得た。そして,振動数条件から得られる光の振動数,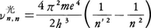 が水素原子のスペクトルとして知られていたバルマー系列(n′=2),パッシェン系列(n′=3)を正しく再現することを示したのである。このボーアの三部作《原子と分子の構成について》は,さらに多電子原子の安定性や分子の結合エネルギーなどを論じている。翌1914年にはJ.フランクとG.ヘルツが電子で原子をたたき,電子のエネルギー損失がちょうど原子の定常状態間のエネルギー差に相当する離散的な値になることを実証した(フランク=ヘルツの実験)。これはエネルギーの離散的な定常状態が光との相互作用に局限されない実在性をもつことを示すものであった。15年にはA.ゾンマーフェルトが量子条件を多重周期の運動に一般化し,水素原子の定常状態をすべて決定した。ここで原子の角運動量が離散的な方向のみをとること(方向量子化)が見いだされ,一方では座標軸は任意の方向に設定できるので,理論はパラドックスに逢着したことになる。
が水素原子のスペクトルとして知られていたバルマー系列(n′=2),パッシェン系列(n′=3)を正しく再現することを示したのである。このボーアの三部作《原子と分子の構成について》は,さらに多電子原子の安定性や分子の結合エネルギーなどを論じている。翌1914年にはJ.フランクとG.ヘルツが電子で原子をたたき,電子のエネルギー損失がちょうど原子の定常状態間のエネルギー差に相当する離散的な値になることを実証した(フランク=ヘルツの実験)。これはエネルギーの離散的な定常状態が光との相互作用に局限されない実在性をもつことを示すものであった。15年にはA.ゾンマーフェルトが量子条件を多重周期の運動に一般化し,水素原子の定常状態をすべて決定した。ここで原子の角運動量が離散的な方向のみをとること(方向量子化)が見いだされ,一方では座標軸は任意の方向に設定できるので,理論はパラドックスに逢着したことになる。
→原子 →原子スペクトル
遷移確率
アインシュタインは原子における一つの定常状態から別の定常状態への電子の遷移は確率的におこるとし,その確率を電子に当たる光の強度に比例する部分(誘導遷移)と光なしでも残る部分(自発遷移)に分けた(1916-17)。ここで,古典統計力学で用いられてきた人間の無知の表現としての確率でなく,内在的な確率が物理学に導入された。その予兆をシュワイドラーが放射性崩壊に見いだしていたことは前に述べた。
対応原理
ボーア=ゾンマーフェルトの理論は,原子の出す光について,その振動数は正しくあたえたが,しかし強度も偏りもあたえることができなかった。ボーアは,たとえば水素原子の場合,電子の軌道が量子数nの増大とともに大きくなり,ついに巨視的となることに注目し,n′=n-τとnの大きい軌道間の遷移で出る光の振動数,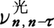 が,古典電磁気学のあたえる振動数,
が,古典電磁気学のあたえる振動数,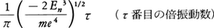 に漸近することを確かめた。このことは,原子サイズの現象を支配する法則の未知の部分も,サイズを大きくした極限で古典的法則につながることを期待させる。ボーアは,これを対応原理とよんで巧妙な推理によって逆向きにつかい,原子が出す光の強度や偏りの公式を,対応する古典的な公式から導き出した。
に漸近することを確かめた。このことは,原子サイズの現象を支配する法則の未知の部分も,サイズを大きくした極限で古典的法則につながることを期待させる。ボーアは,これを対応原理とよんで巧妙な推理によって逆向きにつかい,原子が出す光の強度や偏りの公式を,対応する古典的な公式から導き出した。
マトリックス力学
原子のなかでの電子の定常状態は量子数nで決まる。単位時間当りの公転数もnで決まるνnで,古典的にはこの電子が出す光の振動数はその整数倍のτνnになるが,これは実際にはn→∞で漸近的に正しいだけで(対応原理),原子が出す光の振動数は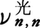 のように二つの整数n,n′で決まる。強度も偏りも同様である。W.ハイゼンベルクは,古典的な量を二つの添字をもつ量の集り{An
のように二つの整数n,n′で決まる。強度も偏りも同様である。W.ハイゼンベルクは,古典的な量を二つの添字をもつ量の集り{An n
n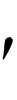 }でおきかえるという方針で,対応原理を推し進め,《運動学的および力学的関係の量子論的解釈変更について》と題する論文(1925)を書いた。ここでは電子の座標も二つの添字をもつ複素数となり,その絶対値の2乗によって光の強度をあたえるという役はするが,もはや軌道運動は記述しない。ハイゼンベルクは〈電子の位置や公転時間のような量を観測するという希望をまったくあきらめ,……観測できる量のみが現れるような力学をつくる〉という立場をとった。彼の見いだした算法は行列算にほかならぬことがわかり,彼の着想はM.ボルンとP.ヨルダンの協力によりマトリックス力学(行列力学)に仕上げられた。マトリックス力学は,水素原子のスペクトルを正しくあたえることが1926年にW.パウリとP.A.M.ディラックとによって証明されたとき,一般に受けいれられた。
}でおきかえるという方針で,対応原理を推し進め,《運動学的および力学的関係の量子論的解釈変更について》と題する論文(1925)を書いた。ここでは電子の座標も二つの添字をもつ複素数となり,その絶対値の2乗によって光の強度をあたえるという役はするが,もはや軌道運動は記述しない。ハイゼンベルクは〈電子の位置や公転時間のような量を観測するという希望をまったくあきらめ,……観測できる量のみが現れるような力学をつくる〉という立場をとった。彼の見いだした算法は行列算にほかならぬことがわかり,彼の着想はM.ボルンとP.ヨルダンの協力によりマトリックス力学(行列力学)に仕上げられた。マトリックス力学は,水素原子のスペクトルを正しくあたえることが1926年にW.パウリとP.A.M.ディラックとによって証明されたとき,一般に受けいれられた。
物質波
1924年,ド・ブロイは光における波動と粒子の二重性を電子にまで及ぼすことを考え,電子は体内振動をもつ粒子だとしてボーアの量子条件に解釈をあたえた。この考えは,結局,エネルギーEと運動量pをもつ電子に振動数ν=E/hと波長λ=h/pの波動を付随させることに落ちつき,この波動は物質波ないしド・ブロイ波とよばれることになった。
波動力学
ド・ブロイは物質波の位相しか問題にしなかった。波動を扱うなら波動方程式をというP.デバイの示唆にこたえて,1926年にE.シュレーディンガーが波動力学をつくった。ここでは電子の定常状態は波の固有振動の形をとるので,彼の四部作は《固有値問題としての量子化》と題されている。ここで彼は,水素原子の問題を解き,それに電場をかけたときにおこるスペクトル線のずれ(シュタルク効果)が古典量子論よりよく説明されることを示すなど多くの成果をあげた。シュレーディンガーは,マトリックス力学が運動の時間的,空間的に連続な記述を断念したことに物理学の武装解除だとして反発し,量子飛躍を波動ψの連続的変化でおきかえようとしたのである。電子のような粒子も,実は空間の小さな領域にかたまってその外では0であるような波動(すなわち波束)であるという波動一元論を主張したが,そのような波束は一瞬のうちに拡散してしまい粒子とはみなせなくなるというローレンツの批判に屈した。それと同じ26年にボルンが波動関数の確率解釈を提出し,これによればシュレーディンガーの方程式からラザフォードの散乱公式が自然に導かれることを示した。こうした成功の反面,たとえばウィルソンの霧箱の中での電子の運動がニュートンの力学で正しく記述される事実との関係が問題になった。27年にハイゼンベルクは不確定性関係を発見して古典力学的記述の適用限界を明らかにし,エーレンフェストは波束ψt(r)の中心の運動が〈それのおかれた力の場の|ψt(r)|2を重みとする平均に等しい力がおこすニュートン力学的運動〉に一致することを証明した。
→不確定性原理
量子力学の成立
1926年,波動力学とマトリックス力学の同等性をシュレーディンガーが示唆した。どちらも同一の構造の異なる表現形式と見るべきもので,それらのほかにも表現形式は無数にあって相互に変換できる。このことをディラックやヨルダンの変換理論が明示したとき量子力学が成立した。ボルンの確率解釈も粒子の位置以外の一般の物理量に拡張されたが,さらに後の観測の理論により補強されねばならなかった。方向量子化のパラドックスはここで解決したのである。量子力学の数学的基礎は,フォン・ノイマンが大枠を描いたが,実質を盛る仕事は原子・分子系のハミルトニアンが自己共役であることを示した加藤敏夫の研究(1955)に始まる。
量子力学の展開
重要な発展の一つは2個以上の粒子を含む系の扱いであり,ここには古典量子論がついに扱いえなかったヘリウム原子の問題が含まれる。1926年から27年にかけてハイゼンベルクとディラックは独立に,粒子の座標の交換に関してフェルミ粒子系の波動関数は反対称(ψ(r1,r2)=-ψ(r2,r1)),ボース粒子系では対称(ψ(r1,r2)=+ψ(r2,r1))となるべきことを導いた。前者はパウリの原理の量子力学的表現であるが,これらの深い意味をパウリが明らかにするのは40年になってからで,それには相対論的な場の理論の発展が必要であった。
こうして量子力学は誕生してから2年たらずで基礎が整い,原子と分子の構造から固体電子論へと華々しい成功の道を進む。原子核への応用は,1928年にG.ガモフがα崩壊をトンネル効果として説明したのが最初であるが,β崩壊の解釈でなぞに出会い核の内部は量子力学の適用限界外かと疑われもした(1931)。
これより先,28年にディラックは電子の波動方程式を相対論の要請にあう形に改め電子のスピンの自然な説明を得たが,負のエネルギーをもつ解があって,その状態に電子が落ちこむという問題に出会うことになった。そして,これらの困難を解決する努力の中から,素粒子論生まれ,場の量子論へと発展することになる。
執筆者:江沢 洋
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「量子力学」の意味・わかりやすい解説
量子力学
りょうしりきがく
quantum mechanics
原子、分子や光などの現象を理解するため、ニュートンの運動法則やマクスウェルの電磁法則などの古典論にかわる新しい運動法則がみいだされ、一つの力学の体系となった。これが量子力学である。
量子力学では古典論と比べて運動状態や物理量の扱い方がまったく異なっている。量子力学における運動状態を量子的状態という。その結果、われわれが日常経験して疑いえないと思われてきた考え方の多くが、原子などの領域でそのままでは成り立たないことが明らかになってきた。微視的という用語は、一般に古典力学あるいは量子力学に従って運動する粒子の集団の状態を個々の粒子の状態にまで立ち入って論ずる場合に用いられるが、この場合、原子、分子や素粒子などの現象が量子力学的に進行することを強調して用いることが多い。微視的に対して巨視的という用語は、個々の粒子の運動に立ち入らずこれら莫大(ばくだい)な数の粒子の集団全体の物理的特徴に注目するとき用いる。この場合、粒子集団の運動は古典的となる。また、量子力学的運動を強調して微視的という用語を用いることが多い。これらの事情のため巨視的という用語は古典論的という意味合いをもっている。微視的をミクロスコピック、巨視的をマクロスコピックという。
[田中 一]
量子力学の誕生
量子力学的法則の認識は1900年のプランクの放射公式に始まるといってよい。この法則の意味をアインシュタインが分析し、この公式が光に波動性と粒子性の二つを同時に付与したことになっていることを示すとともに、光のエネルギー量子、すなわち光量子仮説を提唱した。1913年ボーアは、古典力学を用いて得られる水素原子の電子軌道のうち現実に軌道として可能なものを選択する条件すなわち量子条件と、光放出の新しいメカニズムを導入した。
ハイゼンベルクは1925年ボーアの理論を出発点としてこれを新しい力学につくりかえ、ここに量子力学が誕生した。これとは別に1923年ド・ブローイは電子もまた波動性をもつべきことを予見した。これを一般化して1926年シュレーディンガーが任意のポテンシャルの作用を受けた粒子の波動方程式をみいだした。やがてこの方程式がハイゼンベルクの提起した運動方程式と同等であることが示されて、量子力学の基礎が確立した。
その後今日まで、原子の安定性、原子的見方に基づく物質の性質、原子核、素粒子および宇宙線の現象が量子力学に基づいて研究されてきた。一方、電磁場や中間子場などの場を対象とする量子場、すなわち場の量子論が展開されたが、光の放出・吸収など場に関するさまざまな方程式の解に発散が生ずるなどの困難な問題が現れた。このため量子力学を超える次の理論の試みもしばしば提起された。しかしながら、量子力学の適用の限界を端的に示す事実は現在みいだされていない。
[田中 一]
量子力学の骨組み
水素原子内電子(以下、電子という)は中心の陽子からe2/r2(eは単位電荷、rは電子と陽子間の距離)の引力の作用を受け、その結果-e2/rのポテンシャルエネルギーをもつ。運動エネルギーはp2/2m=(px2+py2+pz2)/2m(mは電子の質量、pxなどはxなどの方向の電子の運動量)であるから、その全エネルギーはp2/2m-e2/rとなる。量子力学ではすべての物理量にそれぞれ演算子が対応している。x方向の運動量の演算子は、-iħ(∂/∂x)(ħはプランク定数hの2π分の1)であって、この結果電子のエネルギーの演算子Hは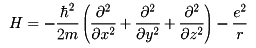
となる。ある定まったエネルギーをもつ電子の量子的状態はH∅(x,y,z)=E∅(x,y,z)という偏微分方程式の解で表される。これがシュレーディンガーの波動方程式である。関数∅を状態関数または波動関数という。この方程式は電子のエネルギーが一定であるという古典力学の関係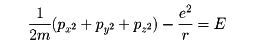
に対応している。
この偏微分方程式を解く場合、状態関数にさまざまな条件を与える。これらの条件は、電子が遠方にまで広がっていないなどの物理的条件に対応するもので、この結果シュレーディンガー方程式の解は常数の位相因子を除いて一義的に決まるが、E<0の解が存在するのはある特定のEの値の場合のみとなる。数学的にいえば、先のシュレーディンガー方程式はエネルギー演算子Hの固有方程式で、関数∅は固有関数、Eは固有値である。∅で表された状態はHの固有状態である。はこうして求めた水素原子のエネルギー値を示す。
同じように量子力学の角運動量は古典力学の角運動量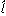 x=ypz-zpyなどの運動量pxなどを微分演算子-iħ(∂/∂x)などで置き換えて得られる(参照)。こうして得られた演算子
x=ypz-zpyなどの運動量pxなどを微分演算子-iħ(∂/∂x)などで置き換えて得られる(参照)。こうして得られた演算子 xなどの2乗の和
xなどの2乗の和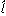 2は角運動量という物理量の大きさの2乗の演算子である。したがって水素原子の場合に限らず角運動量の大きさλの2乗とその状態関数∅は固有値方程式
2は角運動量という物理量の大きさの2乗の演算子である。したがって水素原子の場合に限らず角運動量の大きさλの2乗とその状態関数∅は固有値方程式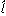 2∅=λ2∅から決まる。∅は特定の角運動量の大きさλをもつ量子的状態を表す。
2∅=λ2∅から決まる。∅は特定の角運動量の大きさλをもつ量子的状態を表す。
粒子はつねに定まった角運動量を有しているとは限らない。水素原子の場合、電子は定まったエネルギーをもつとともに定まった角運動量を有している。このことが可能であるのは、エネルギー演算子Hと角運動量の大きさの2乗の演算子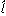 との間に交換可能という特別の関係H
との間に交換可能という特別の関係H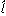 =
=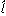 Hが成り立つからで、この関係を可換という。2個の演算子A、Bが共通の固有関数χすなわちAχ=aχ,Bχ=bχをもつための必要十分な条件はAとBとが可換なことである。
Hが成り立つからで、この関係を可換という。2個の演算子A、Bが共通の固有関数χすなわちAχ=aχ,Bχ=bχをもつための必要十分な条件はAとBとが可換なことである。
水素原子内の電子は定まった運動量を有する状態すなわち運動量の固有状態ではない。実際、電子の運動量の演算子-iħ(∂/∂x)などは先ほどのエネルギー演算子Hと交換可能ではない。それではこの場合、電子の運動量はどうなっているのであろうか。運動量の固有関数は-iħ(∂/∂x)∅=px'∅などを満たす。ここでpx'はx方向の運動量の固有値である。この微分方程式は容易に解くことができ、固有関数は波長2πħ/px'の平面波∅px'を表す関数となる。ところで、エネルギーEをもつ電子の状態関数 を、運動量の固有関数の重ね合わせで表すことができる。重ね合わせの係数すなわち重みをa(p)とすれば
を、運動量の固有関数の重ね合わせで表すことができる。重ね合わせの係数すなわち重みをa(p)とすれば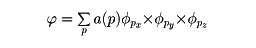
となる。ここでは積分の代わりにΣで表している。このとき電子は運動量pを|a(p)|2の確率で有している。同様に、状態関数 (x,y,z)は電子が点(x,y,z)にある状態関数すなわち位置の固有状態の重ね合わせの係数とも考えられるので、電子は点(x,y,z)に|
(x,y,z)は電子が点(x,y,z)にある状態関数すなわち位置の固有状態の重ね合わせの係数とも考えられるので、電子は点(x,y,z)に| (x,y,z)|2の確率で存在することになる。
(x,y,z)|2の確率で存在することになる。
[田中 一]
量子力学の構成
以上の例にみられた量子力学の原理を以下に列挙しておく。
(1)状態関数 1・
1・ 2を重ね合わせた
2を重ね合わせた =c1
=c1 1+c2
1+c2 2もまた量子的状態を表す状態関数である。
2もまた量子的状態を表す状態関数である。
(2)量子的状態 はχの物理的性質を
はχの物理的性質を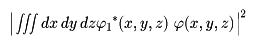
の割合で有している。
(3)物理量は演算子の形をとる。この物理量をオブザーバブルという。オブザーバブルは古典論の物理量の運動量pxなどを-iħ(∂/∂x)などで置き換えて得られる。物理量のとる値はオブザーバブルの固有値のみである。
(4)量子的状態はiħ(∂ /∂t)=H
/∂t)=H に従って時間的に変化する。ここでHはエネルギー演算子で、この方程式もシュレーディンガー方程式という。
に従って時間的に変化する。ここでHはエネルギー演算子で、この方程式もシュレーディンガー方程式という。
運動量pxが微分演算子とすれば、位置xとの間に交換関係xpx-pxx=iħすなわちxpx∅(x)-pxx∅(x)=iħ∅(x)という関係が成り立つ。位置と運動量は特別な関係にある一組の物理量であって、この物理量を用いてニュートンの運動法則を書き換えると、質量すなわち粒子の属性が現れない。位置xと運動量pxのかわりにそれぞれ-pxとxとを用いても同様のことがいえるので、この両者の関係は共役(きょうやく)であることがわかる。この関係を正準共役という。一般に正準共役の関係にある物理量のオブザーバブルA、Bの間にはAB-BA=iħの関係が成り立つ。
状態関数のかわりに演算子が時間的に変化すると考えてシュレーディンガー方程式を書き換え、まったく同じ確率分布を得るようにすることができる。この場合、演算子を行列として表現することが多い。こうして得られた力学の形式を行列力学という。ハイゼンベルクが1925年にみいだしたのは、正準共役な物理量の間の交換関係の行列表現である。
シュレーディンガー方程式を数学的に解くことが困難なため、変分法、ハートリー‐フォックの方法、WKB法、摂動論などさまざまな近似法が用いられる。WKB法は状態関数をプランク定数のべき級数(整級数)展開で求める方法である。
[田中 一]
量子力学運動の特徴
は、電子が水素原子内でとる位置の確率を示している。注意すべきことは、図Bは、電子が瞬間瞬間特定の位置にあってある有限時間にとる電子の位置の全部を図示したもの、すなわち古典統計的な分布を示したものではないということである。この場合、電子は同時に各位置にそれぞれ異なる確率で存在している。運動量についても同様である()。
位置と運動量のオブザーバブルは互いに交換可能ではない。したがって、ある特定の位置を有し、かつ同時にある特定の運動量をもつ量子的状態は存在しない。このことは、古典力学の粒子の状態が位置と運動量とを同時に与えることによって定まるのと比べてきわめて対照的である。一般に粒子はある範囲Δxの位置に同時にあり、かつ、ある範囲Δpxの運動量の値を同時にとる。この場合ΔxとΔpxとの間には不確定性関係ΔxΔpx≧ħ/2が成り立つ。位置の固有状態では位置が定まっているのでΔxは0である。したがってΔpxは∞となり運動量はまったく不確定となる。この不確定性関係は正準共役な二つの物理量の間につねに成り立つ。この不確定性関係は正準関係にある物理量の交換関係から導き出されるものであり、この意味で客観的なものであって、主観の関与によって成り立つものではない。この不確定性関係を粒子の実際の位置の測定に即して示したものがハイゼンベルクのγ(ガンマ)線顕微鏡である()。またの水素原子の状態の位置との運動量分布を一つにまとめると、分布が有限な広がりをもつことがわかる。これは不確定性関係を示す。
一般に対象の測定観測データから対象の状態をみいだす過程の理論を観測の理論という。量子的状態の場合、測定観測装置が古典論の法則に従いながら対象が量子的状態にあるため、この対応にさまざまな問題が生じる。この問題についてアインシュタインとボーアの間で物理的実在に関する論争が行われた。シュレーディンガーのネコ()はこの種の問題の一例であって、主観の客観に対する作用として哲学の論争の材料ともなった。
量子的状態では状態関数の重ね合わせが可能であり、古典的状態は正準共役の物理量の値の組で表現しうるものである。したがって、測定観測過程のどの段階でどのような条件のもとにこの移行が行われたかを、量子力学的過程の結果として示すことが観測の理論の内容であるが、現在まだ十分な解決をみていない。先ほどのネコの例()でいえば、放射線を受けて毒瓶が壊れるという客観的過程によってネコの状態は生と死の状態関数の重ね合わせから、いずれか一方に量子力学的に変化したのであって、この変化は主観に基づくものではない。1990年代になって注目されている量子コンピュータは、情報が重ね合わせ可能であるとして情報変換を行うもので、特定の演算においては現在のスーパーコンピュータよりもはるかに大きな演算速度で行えることが理論的に示されている。このほか、電子あるいは光量子1個の変化による情報処理が構想されている。これらの分野を量子情報とよんでいるが、量子状態を土台とする技術として今後の展開が期待されている。
[田中 一・加藤幾芳]
『天野清著『量子力学史』(1973・中央公論社)』▽『中嶋貞雄著『量子の世界』新版(1975・東京大学出版会)』▽『田中一著『量子の素顔』(1976・大月書店・国民文庫)』▽『町田茂著『基礎量子力学』(1990・丸善)』▽『田中一著『動画付き量子力学』(1991・近代科学社)』▽『原康夫著『岩波基礎物理シリーズ5 量子力学』(1994・岩波書店)』▽『青木亮三著『わかりやすい量子力学』(1994・共立出版)』▽『朝永振一郎著『量子力学2』第2版(1997・みすず書房)』▽『戸田盛和著『量子力学30講』(1999・朝倉書店)』▽『新井朝雄・江沢洋著『量子力学の数学的構造1、2』(1999・朝倉書店)』▽『『朝永振一郎著作集8 量子力学的世界像』(2001・みすず書房)』▽『小出昭一郎・阿部龍蔵監修、江沢洋著『量子力学』全2冊(2002・裳華房)』▽『大高一雄著『基礎量子力学』(2002・丸善)』▽『亀淵迪・表実著『量子力学特論』(2003・朝倉書店)』▽『J・シュウィンガー著、B・G・エングラート編、清水清孝・日向裕訳『シュウィンガー量子力学』(2003・シュプリンガー・フェアラーク東京)』▽『高田健次郎著『わかりやすい量子力学入門――原子の世界の謎を解く』(2003・丸善)』▽『ポール・エードリアン・モリス・ディラック著、朝永振一郎訳『量子力学』(2004・岩波書店)』▽『朝永振一郎著『量子力学と私』(岩波文庫)』

古典力学の物理量と量子力学のオブザーバ…
水素原子のエネルギー準位〔図A〕
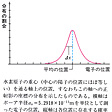
水素原子内電子の位置座標分布〔図B〕
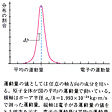
水素原子内の運動量の分布〔図C〕
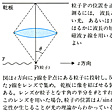
γ線顕微鏡の原理〔図D〕
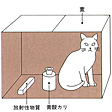
シュレーディンガーのネコ〔図E〕
百科事典マイペディア 「量子力学」の意味・わかりやすい解説
量子力学【りょうしりきがく】
→関連項目位相空間(物理)|因果律|オッペンハイマー|極低温|空孔理論|群論|固体物理学|古典物理学|思考実験|シュタルク効果|シュレーディンガー|ヒルベルト空間|フォン・ノイマン|ホーキング|マクロ(物理)|ミクロ(物理)|力学|量子数|量子電磁力学|量子統計力学
出典 株式会社平凡社百科事典マイペディアについて 情報
化学辞典 第2版 「量子力学」の解説
量子力学
リョウシリキガク
quantum mechanics
ハイゼンベルクの不確定性原理は,原子や分子の世界の現象は古典的な力学理論では記述できないことを示し,この対象に適用される新しい理論体系を追求しなければならなくなった.これが量子力学であり,W.K. Heisenberg,P.A.M. Dirac,E. Schrödinger(1925~1926年)がそれぞれ独立にこれを建設した.それらは外見上の数学的形式はそれぞれ異なっているが,互いに関連しあって物理的内容は同等である.物理学で扱う物理量は,本来,実験によって測定可能な量だけであるから,しばしばオブザーバブルといわれる.原子の世界における電子の場合,系のエネルギーのような量はオブザーバブルとなるが,不確定性原理が示すように電子の位置座標と運動量はともにオブザーバブルにはなりえない.いま,あるオブザーバブルをAで表し,その理論的期待値をaと書く.上記3人はこの期待値aを一定の手順で算出しうる数理的体系をそれぞれ独自の方式で確立した.以下Schrödingerの手法を簡単のため,一粒子系について説明する.
(1)いま問題とする粒子系に対し,その位置座標x,y,zと時間tの関数φ(x,y,z,t)を考える.φがわかると,ある定まった手順の演算をすることにより,オブザーバブルAの期待値aが計算されるほか,この体系のいろいろの量が引き出される.したがって,φをその体系の状態関数または波動関数という.まず束縛された系の状態関数φに対しては自乗積分が可能,
∫ φ*φ dx dy dz = 有限 = 1
という条件が要求される.
(2)次に物理量,つまりオブザーバブルAにはφ(x,y,z,t)に作用するある定まった数学的演算が対応することになるので,以下Aは演算子と考えてよい.
(3)この系におけるあるオブザーバブルの理論的期待値aは,(1),(2)の条件のもとにφλ(x,y,z,t)が満たす固有値問題:
Aφλ = aλφλ
のいくつかある固有値
aλ(λ = 0,1,2,…)
のいずれかである.そして,φはその固有関数φλ である.最後に演算子Aに対するオブザーバブルの測定を何回も繰り返した平均値は,
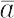 = ∫ φ*Aφ dx dy dz
= ∫ φ*Aφ dx dy dz
で与えられる.
以上が量子力学の3公理である.
(1)においてφ(x,y,z,t)の絶対値の自乗 φ*φは,点(x,y,z)における単位体積当たりの粒子の存在確率を表し,その積分は粒子は空間に広がって存在するが,全体では1個であるというきわめて自然な条件を表している.
(2)におけるオブザーバブルと演算子の対応を比較のため,古典論表示も含めて以下に示す.ただし
ℏ = h/(2π).

h/(2π)の導入は運動量演算子のところとエネルギー演算子でなされ,量子性を反映した状態関数の波動性を示している.
(3)の一例として,粒子の全エネルギーはハミルトニアンを用いて
Hφ = Eφ
の固有値問題として求められる.これをシュレーディンガーの波動方程式といい,粒子運動の基礎方程式である.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
ブリタニカ国際大百科事典 小項目事典 「量子力学」の意味・わかりやすい解説
量子力学
りょうしりきがく
quantum mechanics
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
旺文社世界史事典 三訂版 「量子力学」の解説
量子力学
りょうしりきがく
quantum mechanics
量子の考えはドイツのプランクに始まり,デンマークのボーアによって電子運動の量子化という考えが導入された。その後,オーストリアのシュレディンガー(波動力学),ドイツのハイゼンベルク(マトリックス力学)らによって樹立された。
出典 旺文社世界史事典 三訂版旺文社世界史事典 三訂版について 情報
世界大百科事典(旧版)内の量子力学の言及
【因果律】より
…これらの方程式を解き,ある時刻での初期条件を与えれば,すべての時刻における状態は一義的に決定される。 このような因果関係が物理学を支配していると考えられたが,量子力学の出現によって変更を加えられることになった。原子,分子以下の微視的物体において物理量を測定しようとするとき,その物体の状態を乱さずに観測することができない。…
【応用数学】より
… 応用数学として成功をおさめたものや,現在の課題となっているものの例をあげよう。(1)量子力学,相対論 古典力学から量子力学へと移って,E.シュレーディンガーやW.K.ハイゼンベルクの設定は,数学におけるヒルベルト空間論,作用素の理論,群の表現などの諸概念の重要さに新たな認識が与えられ,種々の研究課題を提供した。一方,中間子論の発展とともに種々の型の場が知られ,素粒子の一般理論が作られ,特殊相対性理論と量子論との要求を満たす理論体系が進むに従って,数学の問題としては,進んだ変分の問題とかローレンツ群の既約表現の問題,S行列の理論などの内容を豊かにした。…
【時間】より
… このように,近代西欧哲学のなかでは,時間は,世界の存在の形式か,世界の存在を支える枠組みか,人間の認識の形式か,いずれにしても人間のいきいきとした〈生〉そのものとは無関係な広域的概念になりつつあったが,それを人間の生の様式へ引き戻そうとしたのが,19世紀末以降のベルグソンによる〈持続〉やフッサール,ハイデッガー,サルトルらの現象学的な〈時間性〉の提案だった。さらに20世紀初頭における相対性理論と量子力学の誕生は,時間概念に決定的な新しい展開を与えた。相対性理論では,絶対時間や絶対的同時性が成立しないことが明らかになった(そこから〈双子のパラドックス〉が生まれる)ばかりではなく,それまで空間と別個の座標軸を与えられていた時間が,空間と独立に扱われるべきでないという新しい事態を迎えたし,量子力学では,エネルギーとペアとなって非可換な2量を構成する時間(物理的観測量としての)が,ハイゼンベルクの不確定性原理を満足すべきものであることが明らかにされ,そこから,一種の〈多時間〉的な発想も生じた。…
【力】より
…電流が磁場をつくることを考えると,電流要素間にも力が働く(ただし,このような力の場合作用反作用の法則は必ずしも成り立たない)ことになるが,この力も遠隔作用と考えるより磁場を通じての近接作用と考えるべきである。
[量子力学的な力]
非相対論的量子力学の世界で電子や原子核の運動を支配しているのはこれらの間のクーロン力である。(万有引力はこの場合クーロン力に比べてけた違いに小さいことがわかっている)。…
※「量子力学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

