フェルミディラック統計（読み）フェルミディラックトウケイ（その他表記）Fermi-Dirac statistics

デジタル大辞泉

フェルミディラック‐とうけい【フェルミディラック統計】

半整数のスピンをもつフェルミ粒子の集まりが示す統計的性質。1926年にイタリアのフェルミと英国のディラックがそれぞれ独立して発見。パウリの原理により、一つの状態に0個または1個の粒子しか占有できない。絶対零度ではエネルギーの低い順から粒子が埋まり、あるエネルギーを超えると粒子が存在せず、その上限をフェルミ準位とよぶ。フェルミ統計。→ボースアインシュタイン統計

出典　小学館

日本大百科全書(ニッポニカ)

フェルミ‐ディラック統計
ふぇるみでぃらっくとうけい
Fermi-Dirac statistics

多数の粒子の運動を統計的に扱って、その系の性質を表現する方法の一つ。イタリアのフェルミおよびイギリスのディラックがそれぞれ独立に考えた。単にフェルミ統計ともいう。

　同種粒子N個からなる系を扱う場合、粒子間に働く相互作用が非常に小さいとみなせるならば、粒子は独立の運動をすると考えられる。この粒子の運動は、量子力学では1粒子に対するシュレーディンガー方程式を満たす波動関数として記述できる（これを1粒子状態という）。それらをエネルギーの低いものから順に番号づけし、エネルギーの値をε₁、ε₂、……とする。各粒子はこれらの許される状態のどれか一つをとる。量子力学では同種粒子の区別はできないので、N粒子からなる一つの量子状態は、各1粒子状態に粒子が何個ずつ入っているかによって指定される。この数を占有数という。この占有数が0または1しか許されない場合をフェルミ統計という。つまり二つ以上の粒子は、同じ状態になれないことを意味する（パウリの原理または禁制則が成り立つ）。このようなフェルミ統計に従う粒子を、フェルミ粒子またはフェルミオンという。半整数つまり1/2、3/2、……のスピンをもつ粒子、たとえば電子、陽子、中性子、ヘリウム3などがフェルミ粒子である。

　ここで使われる1粒子状態は、ポテンシャルが平坦な場合は平面波となる。また、結晶中の電子などの場合には、イオンのつくる周期ポテンシャルをもつシュレーディンガー方程式を満たす波動関数を1粒子状態とすればよい。また粒子間相互作用がある場合でも、他の粒子からの相互作用の合計を平均したもの（平均場）を考えて、すべての粒子に共通な1粒子シュレーディンガー方程式を解くという近似も可能である（一体近似という）。

　以上では、1粒子状態の占有数ということからフェルミ統計を定義したが、もう少し一般的な意味でフェルミ統計を使うことがある。一般にN粒子の波動関数中の二つの粒子の座標（およびスピン）を交換すると、元と同じ波動関数になるか（対称であるという）、「-1」倍されるか（反対称という）の2通りしか許されない（空間3次元の場合）。反対称な場合、粒子はフェルミ統計に従うという（対称な場合は、ボース‐アインシュタイン統計）。波動関数を1粒子状態で記述した場合、この一般的なフェルミ統計の性質から、占有数が0か1に限られるという結果が得られる。

　フェルミ統計に従う粒子系が絶対温度Tの熱浴（物体と接触して熱のやりとりをする外界）と粒子浴（物体と接触して粒子のやりとりをする外界）に接しているとして統計力学的に扱うと、エネルギーεをもつ粒子数の平均値は
　　f(ε)＝1/[e^(ε-μ)/kT＋1]
で与えられることが示される。これをフェルミ分布関数といい、kはボルツマン定数、μは化学ポテンシャルである。

［小形正男］

[参照項目] | 素粒子 | ディラック | 伝導電子 | 統計力学 | パウリの原理 | フェルミ | フェルミ準位 | ボルツマン定数

出典　小学館　日本大百科全書(ニッポニカ)

法則の辞典

フェルミ‐ディラック統計【Fermi-Dirac statistics】

半整数スピンをもった互いに相似な粒子よりなる集合の統計．このような粒子の系は，粒子の入れ替えに関して反対称の波動関数をもち，またパウリの排他原理を満足しているから，一つの状態に最大1個の粒子しか入りえない．エネルギー E の状態を占める確率 f（E） は

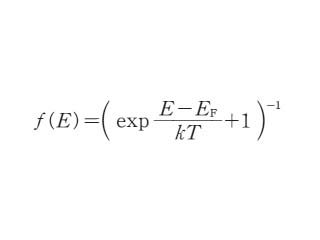
で与えられる．この式はよくフェルミ‐ディラックの分布則＊と呼ばれている．E_F はフェルミエネルギー＊で，占有確率が1/2となるエネルギーに等しい．

出典　朝倉書店

改訂新版　世界大百科事典

フェルミ=ディラック統計 (フェルミディラックとうけい)

→量子統計

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

フェルミ＝ディラック統計
フェルミディラックとうけい

「フェルミ統計」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のフェルミディラック統計の言及

【量子統計】より

…ボース粒子は，2粒子交換で波動関数が(符号を含め)まったく不変であるような粒子のことであり，これにはスピンが整数の素粒子や複合粒子，すなわちπ中間子，フォトン，質量数が偶数の原子核などが属する。このことから，フェルミ粒子の場合は一つの粒子状態を占める粒子数は0または1に限られる(フェルミ=ディラック統計，またはフェルミ統計という)。一方，ボース粒子の場合は一つの粒子状態が収容できる粒子数は0,1,2,3，……と限りがない(ボース=アインシュタイン統計，またはボース統計という)。…

※「フェルミディラック統計」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」