ナビエストークスの方程式（読み）ナビエストークスノホウテイシキ

デジタル大辞泉

ナビエストークス‐の‐ほうていしき〔‐ハウテイシキ〕【ナビエストークスの方程式】

流体力学における基礎方程式の一。粘性流体のふるまいを記述する運動方程式であり、質量×加速度＝重力＋圧力勾配＋粘性力で表される2階非線形偏微分方程式の形式をもつ。19世紀にH＝ナビエ、G＝ストークスにより導出された。

出典　小学館

化学辞典 第2版

ナビエ-ストークスの方程式
ナビエストークスノホウテイシキ
Navier-Stokes' equation

ニュートン流体における，ナビエ-ストークスの(運動)方程式は，

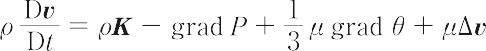
で表される．流体の密度をρ，粘度をμ(一定)，速度をv(u，v，w)，圧力をP，流体の単位質量にはたらく力をK(X，Y，Z)とすれば，粘性流体の運動方程式(コーシーの運動方程式，応用方程式)に，ニュートン流体の応力とひずみ速度の関係を代入して得られる．非圧縮性流体では，右辺第3項が0となり，

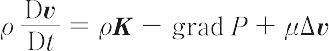
となる．ここで，

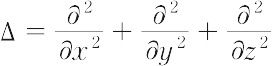
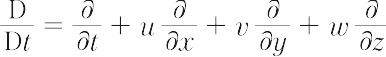
である．ナビエ-ストークスの(運動)方程式で，μ ＝ 0とおけば，完全流体に対するオイラーの運動方程式が得られる．また，この式は簡単化され，プラントルの境界層方程式の導出にも役立っている．

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内のナビエストークスの方程式の言及

【流体力学】より

…　ニュートンの粘性法則に従う粘性流体の基礎方程式が導出され，実在の流体が粘性をもつことによる実験的事実を解明する基礎がきづかれるには，フランスのナビエLouis Marie Henri Navier(1785‐1836)，G.G.ストークスを待たなければならなかった。ナビエ=ストークスの方程式がこれであって，オイラーの方程式を粘性0の特別な場合として含む，単純な流体に対する流体力学の基礎方程式がここに完成した。ただし方程式の非線形性のために，ストークスの近似の成り立つ，慣性項と粘性項の比(レーノルズ数といい，R_eで表す)が小さい場合を除いては数値的な解法が必要であり，またR_eが大きくなると，O.レーノルズが円管内の流れの実験でみいだしたように整然とした層流から時空的に不規則で乱れた乱流に移行するという乱流解が含まれている。…

※「ナビエストークスの方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」