バリオグラム（その他表記）variogram

最新 地学事典

バリオグラム

variogram

地球統計学の基本的概念の一つ。距離がh離れた2地点における値の差の平方和の平均。測点x_iにおける値をw（x_i）測点x_i＋hにおける値をw（x_i＋h）とし，測点対の数をn（h），バリオグラムをγ（h）と書くと，γ（h）＝Σ｛w（x_i）－w（x_i＋h）｝²/n（h）で定義される。この値の半分をセミバリオグラムという。また単にこれをバリオグラムということもある（以下はこの定義に従う）。全データの不偏分散をV, 測点間距離を変数とする自己相関係数をr（h）とすると，γ（h）＝V｛1－r（h）｝という関係が成り立つ。バリオグラムの値は，通常距離の増加とともに増加する。距離がある値以上になると，バリオグラムの値はほぼ一定になる。この一定値をシル（sill：N＋S），シルに達したときの距離をレンジ（range：a）という。測点間隔がレンジを越えると，データ間には相関がない。バリオグラムに適当な連続関数を当てはめたとき，関数が原点を通らず，距離0である値をとることがある。これをナゲット効果（Nugget effect : N）という。当てはめに最もよく利用される連続関数は，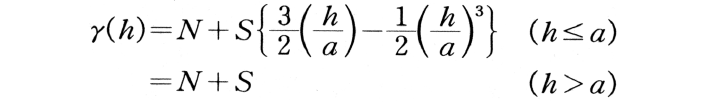

で，球モデルと呼ばれる。空間的にデータの連続性がよいとレンジが大きく，連続性が悪いとレンジが小さい。二次元あるいは三次元のバリオグラムが描かれると，空間における連続性のよい方向と悪い方向を知ることができる。

執筆者：正路 徹也

出典　平凡社「最新 地学事典」

ブリタニカ国際大百科事典 小項目事典

バリオグラム
variogram

空間座標に規制された変量のばらつきをベクトルの関数として求める方法。金属鉱床の品位のばらつきを把握する方法として開発された。

出典　ブリタニカ国際大百科事典 小項目事典