モールの応力円（英語表記）Mohr's stress circle

法則の辞典

モールの応力円【Mohr's stress circle】

主応力が既知の場合に，横断面の応力を決定できるような作図である．弾性体内のある一点において任意の傾きをなす断面に作用する垂直応力およびずり応力を図面上で求めることが可能である．

二次元物体中で，任意の点において主応力 σ₁，σ₂ が与えられているとする．法線方向がσ₁ と θ の角度をなす面上では，垂直応力は

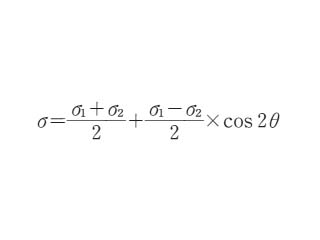
となる．一方，ずり応力 τ は

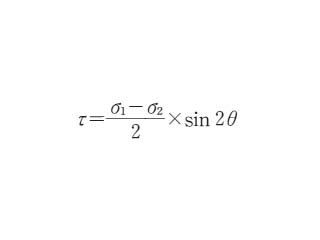
となるので，この両方から θ を消去すると

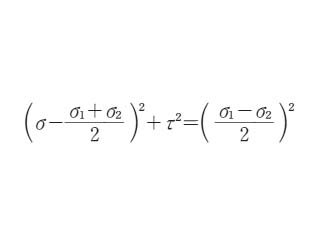
となる．これは横軸に σ，縦軸に τ をとると，中心座標（（σ₁＋σ₂）/2，0），半径 |（σ₁－σ₂）/2 | の円となる．この円が，モールの応力円と呼ばれるもので，傾き θ の断面に作用する力は，円の中心を通り σ 軸から下向きに2θ だけの角度の直線をひいて，円周との交点の座標から得られる．

出典　朝倉書店

世界大百科事典（旧版）内のモールの応力円の言及

【粉粒体】より

…粉粒体の内部における主応力をσ₁,σ₂とすれば，この円の上の任意の点Pのσ,τ座標値は，粉粒体内部の任意の面に対して作用する垂直応力とせん断応力の関係を満足している。このような円は粉粒体(あるいは一般に固体)の内部の応力状態を表しており，モールの応力円，またはモール円と呼ばれる。粉粒体が滑りを起こす限界応力状態に対応するモール円をいくつも描くと，その包絡線が得られる。…

※「モールの応力円」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」