クライン=ゴルドン方程式（読み）クライン＝ゴルドンほうていしき（その他表記）Klein-Gordon equation

ブリタニカ国際大百科事典 小項目事典

クライン＝ゴルドン方程式
クライン＝ゴルドンほうていしき
Klein-Gordon equation

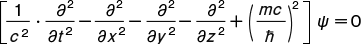真空中を単独で運動する粒子が従う相対論的波動方程式。相対性理論によれば，自由粒子のエネルギー E，運動量 p，静止質量 m の間には普遍的な関係式 E²－p²c²＝m²c⁴が成り立つ（c は光速度）。量子力学の一般的処方に従って E と p を演算子で置き換えると，この関係から次のクライン＝ゴルドン方程式が得られる。ψは自由粒子の波動関数または場の演算子であり，また ℏ＝h/2π はプランク定数である。スピン 0の場は（アイソスピンなどの自由度を別にすれば）1成分で，この方程式を満たす。スピンが 0でない場のψは多成分で，基本的にはもっと複雑な方程式に従うが，それを変形してψはこのクライン＝ゴルドン方程式を満たす必要のあることが示される（→ディラック方程式）。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

クライン‐ゴルドン方程式【Klein-Gordon equation】

もともと弾性媒質中にあるしなやかな弦の運動を記述した微分方程式で

のように書ける．量子力学においては，スカラー中間子（スピンのない中間子）を記述するのに用いられる．

出典　朝倉書店