波動方程式（読み）ハドウホウテイシキ（英語表記）wave equation

デジタル大辞泉

はどう‐ほうていしき〔‐ハウテイシキ〕【波動方程式】

電磁波・弾性波などの波動に関する運動方程式。空間座標と時間とを独立変数とする偏微分方程式。量子力学では粒子の運動状態を記述する方程式をいう。1926年にシュレーディンガーが確立した。

出典　小学館

精選版 日本国語大辞典

はどう‐ほうていしき‥ハウテイシキ【波動方程式】

1. 〘 名詞 〙
2. ① 波動を表わす方程式。媒質の状態を位置と時間との関数とみたとき、これが満たす二次の偏微分方程式をいう。
3. ② 量子力学で物質波の波動関数を記述する微分方程式。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

波動方程式
はどうほうていしき
wave equation

二階線形双曲型方程式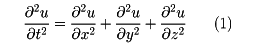

を波動方程式という。f(x,y,z)が3回連続的微分可能、g(x,y,z)が2回連続的微分可能ならば、（1）の初期条件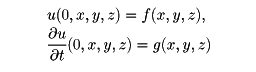

を満たす解はただ一つ存在して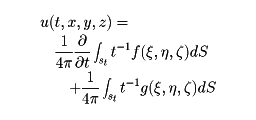

で与えられる（キルヒホッフの公式）。ここでS_tは(ξ,η,ζ)空間の(x,y,z)を中心とする半径tの球面、dSはその上の面素である。空間二次元、一次元の場合の解はそれぞれ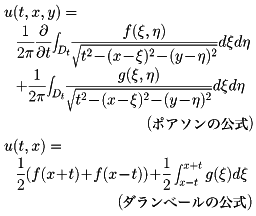

で与えられる。ただし、D_tは原点を中心とする半径tの円である。

［小林良和］

物理学における波動方程式

一般に波においては、媒質の変位や、電場、磁場の成分のような物理量uが波動方程式とよばれる二階の偏微分方程式を満足する。波動方程式を満足する関数uは波動関数とよばれる。

　x方向に進行する波については、波動関数u(x,t)の時間tに関する二階の偏微分係数∂²u/∂t²が、位置座標xに関する二階の偏微分係数∂²u/∂x²に比例する。すなわち∂²u/∂t²=v²(∂²u/∂x²)で、これが（一次元の）波動方程式である。比例係数v²のvは波の伝わる速度である。この偏微分方程式の一般解は、
　u=u₁+u₂,u₁=f(t-x/v),u₂=g(t+x/v)
と書ける。ここに、fとgは、任意の関数である。u₁はプラスx方向に、u₂はマイナスx方向に、いずれも速度vで伝わる波を表す。一般には、時刻tに、位置座標(x,y,z)の点における波動関数u(x,y,z,t)は、波動方程式
　　∂²u/∂t²
　　　=v²(∂²u/∂x²+∂²u/∂y²
　　　+∂²u/∂z²)
を満足する。

［飼沼芳郎］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

波動方程式 (はどうほうていしき)
wave equation

位置座標x，y，zと時間tに関する2階線形偏微分方程式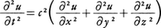，を波動方程式という。この方程式を満足する関数u（x，y，z，t）は速さcで進む波の性質をもつ。例えば関数，

　u＝f（lx＋my＋nz∓ct）　（l²＋m²＋n²＝1）　

は上の方程式を満足するが，この関数はx軸，y軸，z軸となす角の余弦がそれぞれl，m，nで与えられる方向に進む平面波を表す。波動が起こる現象では，波として伝わる物理量の従う方程式が波動方程式の形をもつ。なお波動力学では粒子のふるまいを表す波動関数を定める方程式を波動方程式という。この方程式はシュレーディンガー方程式とも呼ばれており，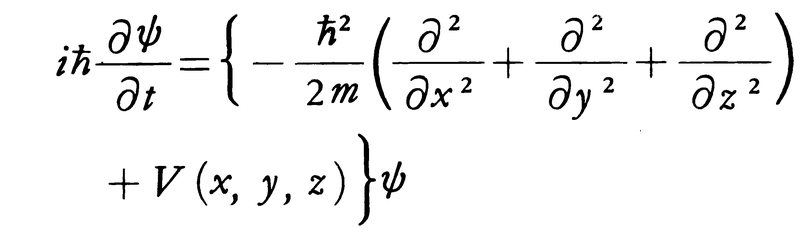

の形をもつ。ここでiは虚数単位，ħはプランク定数hを2πで割ったもの，mは粒子の質量，V（x，y，z）は位置エネルギーを表す。
→波動　→波動力学
執筆者：有山 正孝

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

波動方程式
はどうほうていしき
wave equation

一般には，波を記述する偏微分方程式をいう。一様な媒質中を伝わる波の振動状態を表わす変数 f は，波動方程式 ∂²f/∂t²＝v²△f ( △ はラプラシアン ) を満足する。ここで v は波の速度を表わす。波動方程式の解は前進波と後退波の和によって与えられる。狭義には，量子力学におけるシュレーディンガーの波動方程式をさす。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

波動方程式【wave equation】

通常の物理・化学分野ではほとんどの場合シュレーディンガーの波動方程式＊のみを意味するが，地球物理学では地震波を扱う方程式を同じように，波動方程式という．

出典　朝倉書店

世界大百科事典（旧版）内の波動方程式の言及

【波動】より

…電磁波は電磁誘導によって次々に磁場，電場が変化することによって伝わる。
［波動方程式］
　波動を理論的に取り扱うためには，まずそれを数式的に表現することが必要である。x軸の正の向きに進む波の形は，位置xと時間tの関数u(x,t)で表すことができる。…

【偏微分方程式】より

…
［振動･波動の問題］
　振動，または波動の現象では，時刻tにおける点xの変位u(t,x)があまり大きくないときは，それが時間tとともに変化する状態は次の方程式で記述される。この形の方程式を双曲型方程式，または波動方程式という。　(4)においてfが変数tを含まない場合で，温度が平衡状態にあるとき，すなわちuが時間とともに変化しないときは，∂u/∂t＝0であるから，(1/c)f(x)をあらためてf(x)と書けば，(4)は，　Δu＝－fとなる。…

※「波動方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」